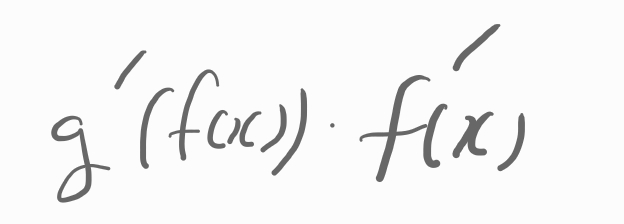함수가 실수 전체의 집합에서 연속이라면x가 -2일 때의 좌극한과 우극한값이 같아야 합니다.문제의 조건을 풀어서 다시 적어본다면,5 ×(-2)+a=(-2)²-a입니다.정리하자면2a=4+10a를 구할 수 있습니다. 참고로 24학년도 수학 4번을 링크합니다.https://blogger3036.tistory.com/21 24학년도 수학4번네 번째 문제입니다. 함수의 연속문제입니다.x값 2를 기점으로 좌우 함수가 다릅니다.x가 2보다 작을 때는 일차함수,x가 2보다 크거나 같을 때는 2차함수입니다.대충 함수를 그려 봅니다.이 함수blog.urno.co.kr