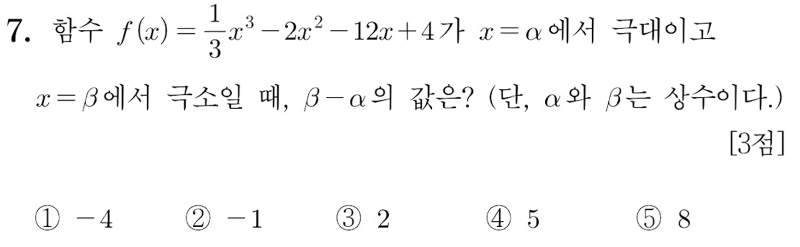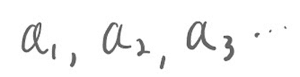JOB생각

18번째 문제입니다.수열들의 연산(?) 문제입니다. 첫 번째 조건에서는a1 + a2 + a3 + a4 + a5 + a6 + a7 + a8 + a9 + a10 이(2 ×b1 - 1) + (2 ×b2 - 1) + (2 ×b3 - 1) + (2 ×b4 - 1) + (2 ×b5 - 1) + (2 ×b6 - 1) + (2 ×b7 - 1) + (2 ×b8 - 1) + (2 ×b9 - 1) + (2 ×b10 - 1)과 같다고 했습니다. 조금 간단히 써보겠습니다.   두 번째 조건은, 입니다.첫 번째 조건을 이용해서 에 관한 식으로 두 번째 조건식을 정리해 봅니다. 괄호를 풀어서 정리해 봅니다.... 이제,1항부터 10까지의 수열 bn의 합을 구할 수가 있습니다.

x가 1일 때의 f(x)의 미분값을 구하는 문제입니다.다항함수의 곱으로 표현되어 있기 때문에 바로 미분이 어렵습니다.그래서 함수 f(x)를 풀어헤쳐 봅니다.이제 미분을 해봅니다.답이 구해졌습니다.그런데 사실,f(x)를 전개하지 않아도 미분을 할 수 있습니다.두 함수의 곱으로 표현된 함수의 미분은이런 방식으로 미분할 수 있습니다.두 함수의 곱으로 표현된 함수를 p(x)라고 해봅니다.p(x)의 도함수(미분함수)는입니다. 이 식을 f(x)와 g(x)에 대한 식으로 다시 정리해 봅니다. ... ......... 거의 정리가 되었습니다. 이제 곱으로 표현된 함수의 미분을 조금 더 쉽게 풀 수 있습니다. 이미 답을 구했지만, 지금 정리한 미분방법으로 다시 풀어봅니다. ... 식을 전개해서 풀었던 때랑 결과가 ..

이제 주관식 문제입니다.배점이 3점...뭔가 난도가 내려간 느낌입니다.항등식이기 때문에왼쪽과 오른쪽이 같은지 확인하면 될 것 같습니다. 주어진 식을 정리해 봅니다.  항등식이기 때문에양쪽의 지수가 같습니다.x-8 = -3x4x = 8 x값을 간단히 구할 수 있습니다. 끝.

오블완은 끝이 났지만,계속 이어서 풀어봅니다.  첫 번째 항이 자연수,{an} 수열을 문제에서 주어진 조건에 맞게 나열해 봅니다.나열하다가 보면 어떤 규칙이 보이겠지 싶습니다.우선 제일 작은 자연수 1을 첫 번째 항이라고 임의로 정해봅니다. a1 = 1a2 = 2a3 = 1a4 = 2a5 = 1... 전체적으로 좀 정리를 해야겠습니다.엑셀의 도움을 받습니다.a1a2a3a4a5a6a71212121212121238421214212121532168421638421271286432164284212129512256128643216105321684211204810245122561286412638421138192     147128643216415      1684212117      189512    19     ..

f(x) 함수는 3차 함수입니다.대충 그려봅니다.f(x)가 0이 되는 점들이 우선 눈에 보이네요.내친김에 극대점을 찾아봅니다.t가 0과 6 사이의 실수라고 했기 때문에x가 6보다 큰 극소점은 신경 쓰지 않겠습니다.0과 6 사이에 극대가 있다면,그림으로 봤을 때 아마도 x가 3일 때 일거라 짐작해 봅니다.혹시 모르니, 확인을 위해서 f(x)를 미분해 봅니다.이대로는 미분이 어려워서식을 정리해 봅니다.미분하기 쉬운 형태가 되었습니다.x² - 10x + 18 이 0이 되는 x값을 찾아야 하는데인수분해가 되는 모양이 아닙니다.x가 정수가 아니었네요.근의공식을 이용해 계산해 봅니다....함수 f(x)의 극대는 처음 예상했던 x가 3일 때가 아니었습니다. 이렇게 되면 다른 풀이방법을 찾아야 할 것 같습니다.{무리수..

등차수열...입니다.각 항을 나열해 봅니다.문제에서는 6번째 항의 절댓값과 8번째 항이 같다고 했습니다.그렇다면 6번째 항은 음수입니다.왜냐하면첫째, 6번째 항이 양수이고 8번째 항도 양수라면등차수열이 될 수 없고,둘째, 6번째 항이 양수이고 8번째 항이 음수라면 위의 등식이 성립하지 않습니다.셋째, 6번째 항과 8번째 항 모두 음수인 경우에도 위의 등식이 성립하지 않습니다.절댓값을 풀어서 계산해 봅니다.- ( a + 5d ) = a + 7da = - 6d첫 번째 항을 알았으니 수열의 다시 나열해 봅니다.-6d, -5d, -4d, -3d, -2d, -d, 0, d, 2d...6번째 항은 -d였고8번째 항은 d였습니다.|-d| = d조건을 만족하네요..  이제 다음 조건을 살펴보겠습니다.k가 1일 때부터 ..

수직선 위의 두 점을 일단 그려보겠습니다. 점 P와 점 Q 사이에 점 1이 있고 점 1과 점 P사이의 거리와 점 Q와 점 1 사이의 거리의 비가 m : 1-m 이라고 합니다. 식으로 표현해보면, 이런 식을 얻을 수 있습니다. {뭔가 복잡한 계산이 될 것 같아 짜증이 좀 납니다.} 계산을 계속해봅니다. . . .. . . . . . 무언가 정리가 되고 있는 듯합니다. 이렇게 계산을 해나가다 보니, 애초에 문제 무엇이었는지 궁금해집니다. 아...! 4의 m제곱을 구하는 거였습니다. 정리하던 식을 조금 더 정리 해봅니다. 3분의 12는 4이니까..., 양변을 비교해서, 4의 m제곱의 값을 구할 수 있습니다. 끝.

뚫어져라 쳐다보니, 식을 정리하면 뭔가 보일 듯싶습니다. 왼쪽을 f(x)로 묶어봅니다. f(x) × (x - 1) 오른쪽을 3x로 묶어봅니다. 3x × (x³ - 1) x³ - 1 = (x - 1) × (x² + x + 1) 입니다. 다시 전체식을 써보면, f(x)(x-1) = 3x(x-1)(x²+x+1) 입니다. 양변에 똑같은 (x-1)을 지워봅니다. 이제 함수 f(x)가 보입니다. f(x) = 3x(x²+x+1) 이제,이 값을 구 할 수 있을 듯싶습니다. 그러기 위해서 다시 함수 f(x)를 풀어헤쳐봅니다. f(x)는... 계산의 편의를 위해서 3은 적분식에서 빼줍니다. {나중에 곱해주면 됩니다.} 정적분을 해봅니다. 빼고 더하고 하니 3 곱하기 3분의 16이 남습니다. 답이 구해졌습니다.

24학년도 수학7번 문제입니다. 함수 f(x)가 3차함수입니다. 최고차항은 3분의1 x의 세제곱, 최고차항의 계수는3분의 1입니다. 최고차항의 계수가 양수이기 때문에 오른쪽으로 증가하는 모양을 가지는 함수입니다. 그리고 극대와 극소가 있다고 하니, 아마도 대충 이런 모양을 하고 있을 것 같습니다. 3차함수의 일반적인 모습입니다. 극대와 극소를 구분해 보면, x가 α 일 때 극대, x가 β 일 때 극소를 갖습니다. 보이는 것과 같이 β 가 α 보다 큽니다. α < β 그리고 극대와 극소에서의 접선의 기울기는 0입니다. 그러니까 f(x)를 미분해서 값이 0인 x값 α 와 β 를 찾으면 될 거 같습니다. f(x)를 미분해 봅니다. 인수분해를 해 봅니다. 이제 그림을 그려봅니다. 3차함수 f(x)를 미분한 값은..

벌써 6번 문제입니다. 아니 아직 6번 문제인 거 같습니다. 등비수열... 입니다. 첫 번째 항과 두 번째 항의 합을 구해야 합니다. 그러기 위해서는 , 일반항an을 알아야 합니다. 등비수열은 수열이 같은 비율로 커지거나 작아지는 수열입니다. 그래서 첫 번째 항을 a라고 하고 등비를 r이라고 한다면, a1, a2, a3, ... , an 은입니다. 그런데... 문제를 보니 다뤄야 할 항이 겨우 다섯 개입니다. 그래서 그냥 나열해 봅니다. a, ar, ar², ar³, ar⁴ 첫 항부터 4번째 항까지의 합 a + ar + ar² + ar³ 에서 첫 항부터 2번째 항까지의 합 a + ar 을 빼면 ar² + ar³인데 문제에서는 이 값이 네 번째 항에 3을 곱한 값과 같다고 합니다. ar² + ar³ = 3..