JOB생각

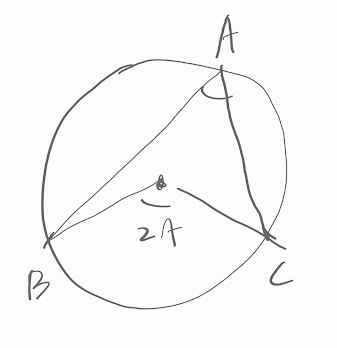
삼각형의 넓이는 밑변 × 높이 ÷ 2입니다.누구나 다 아는 불변의 진리입니다. 오늘은 삼각형의 넓이를 조금 다르게 정리해 봅니다.  삼각형의 넓이 S는 밑변 × 높이 ÷ 2 높이 h는 입니다. 그래서 삼각형 넓이 S를 다시 정리하면,입니다. 그런데, 입니다.이전 글에서 정리했었던 관계식입니다.   이 관계식을 정리하면, sinB를 얻을 수 있습니다. 그러면, 삼각형의 넓이를  다르게 표현할 수 있습니다.  삼각형의 넓이는밑변 × 높이 ÷ 2이지만,세 변의 길이를 모두 곱합값을 외접원의 반지름의 길이의 4배로 나눈값이기도 합니다.S = (a × b × c) ÷ 4R 이제 외접원의 반지름과 세변의 길이를 이용해서 구할 수 도 있게 되었습니다.

지난 글에서 삼각형의 점들 중 어느 한 점을 외접원의 중심으로 옮기면 각도가 2배가 된다는 사실을 정리했었습니다.오늘은 외접원의 원점을 지나는 변을 갖는 삼각형이 왜 직각삼각형이 되는지 정리해 보겠습니다.https://blogger3036.tistory.com/32 삼각형, 외접원, 반지름, 삼각형의 내각과 대응변의 관계모든 삼각형은 하나의 외접원을 가지고 있습니다. 외접원의 반지름의 길이를 R이라고 할 때 모든 꼭짓점(A, B, C)에서 원의 중심 O까지의 거리는 모두 같습니다.(반지름 R)또 삼각형 ABO, 삼각형 Ablogger3036.tistory.com 지난번과 마찬가지로 기하학적 접근이 제일 정리하기 쉬울 것 같습니다.삼각형 ABO, 삼각형 AOC는 모두 이등변삼각형입니다. 각 AOB는 삼..

모든 삼각형은 하나의 외접원을 가지고 있습니다. 외접원의 반지름의 길이를 R이라고 할 때  모든 꼭짓점(A, B, C)에서 원의 중심 O까지의 거리는 모두 같습니다.(반지름 R)또 삼각형 ABO, 삼각형 ACO, 삼각형 BCO 모두 이등변삼각형입니다. 각 BOC를 구해보자면,2π - (각 AOB + 각 AOC)각 AOB = π - 2 ○ 각 AOC = π - 2 ☆  정리해서 풀어보면,각 BOC = 2π - π + 2 ○ - π + 2 ☆ = 2( ○ + ☆)입니다.그런데, 각 ( ○ + ☆)는 ∠ A (각 BAC)이었습니다. 그렇습니다. 삼각형에서 어느 한 점을 외접원의 원점으로 옮기면...각도가 2배가 됩니다.    각 BOC는 각 BAC의 2배입니다.(2 × ∠ A) 그리고 삼각형 BOC는 이등변삼..