반응형
지난 글에서 삼각형의 점들 중 어느 한 점을 외접원의 중심으로 옮기면 각도가 2배가 된다는 사실을 정리했었습니다.
오늘은 외접원의 원점을 지나는 변을 갖는 삼각형이 왜 직각삼각형이 되는지 정리해 보겠습니다.
https://blogger3036.tistory.com/32
삼각형, 외접원, 반지름, 삼각형의 내각과 대응변의 관계
모든 삼각형은 하나의 외접원을 가지고 있습니다. 외접원의 반지름의 길이를 R이라고 할 때 모든 꼭짓점(A, B, C)에서 원의 중심 O까지의 거리는 모두 같습니다.(반지름 R)또 삼각형 ABO, 삼각형 A
blogger3036.tistory.com

지난번과 마찬가지로 기하학적 접근이 제일 정리하기 쉬울 것 같습니다.
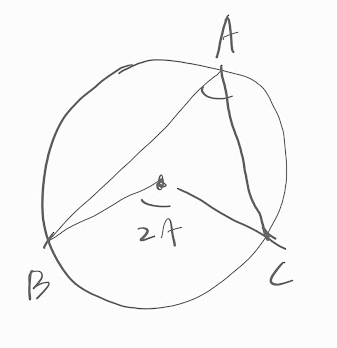
삼각형 ABO, 삼각형 AOC는 모두 이등변삼각형입니다.
각 AOB는 삼각형 AOB의 나머지 각으로 π - (2 ×○)입니다.
그래서 각 AOC는 직선의 각 π에서 각 AOB를 뺀
π - { π - (2 ×○)}입니다.
정리하면, 2 ×○입니다.
그래서 삼각형 AOC의 모든 각을 합한 것은
( 2 ×○) + ( 2 × ☆) = π이고,
식을 정리하면,
2( ○ + ☆) = π
○ + ☆ = π/2
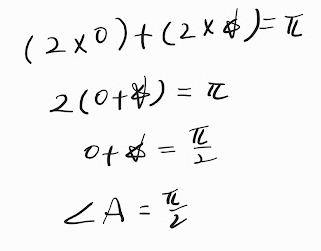
90도(직각)입니다.
그래서 삼각형의 한 변이 외접원의 원점을 지난다면,
그 삼각형은 직각삼각형입니다. 정리를 마칩니다.
'math' 카테고리의 다른 글
| 24학년도 수학13번 (1) | 2024.11.26 |
|---|---|
| 삼각형의 외접원, 외접원의 반지름, 삼각형의 넓이 (0) | 2024.11.25 |
| 삼각형, 외접원, 반지름, 삼각형의 내각과 대응변의 관계 (0) | 2024.11.23 |
| 24학년도 수학12번 (0) | 2024.11.21 |
| 24학년도 수학11번 (0) | 2024.11.20 |