반응형

x가 1일 때의 f(x)의 미분값을 구하는 문제입니다.
다항함수의 곱으로 표현되어 있기 때문에 바로 미분이 어렵습니다.
그래서 함수 f(x)를 풀어헤쳐 봅니다.

이제 미분을 해봅니다.
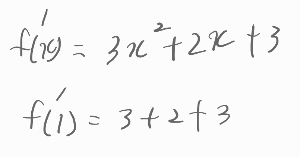
답이 구해졌습니다.
그런데 사실,
f(x)를 전개하지 않아도 미분을 할 수 있습니다.
두 함수의 곱으로 표현된 함수의 미분은
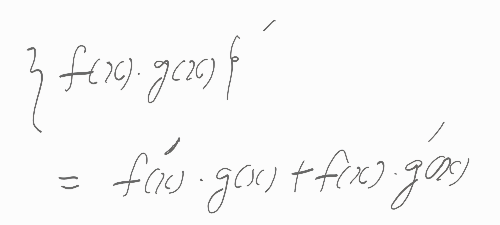
이런 방식으로 미분할 수 있습니다.
두 함수의 곱으로 표현된 함수를 p(x)라고 해봅니다.
p(x)의 도함수(미분함수)는

입니다.
이 식을 f(x)와 g(x)에 대한 식으로 다시 정리해 봅니다.
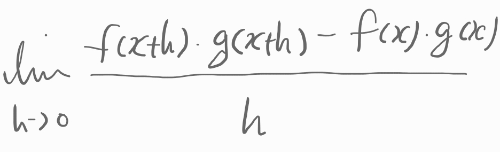

.
.
.
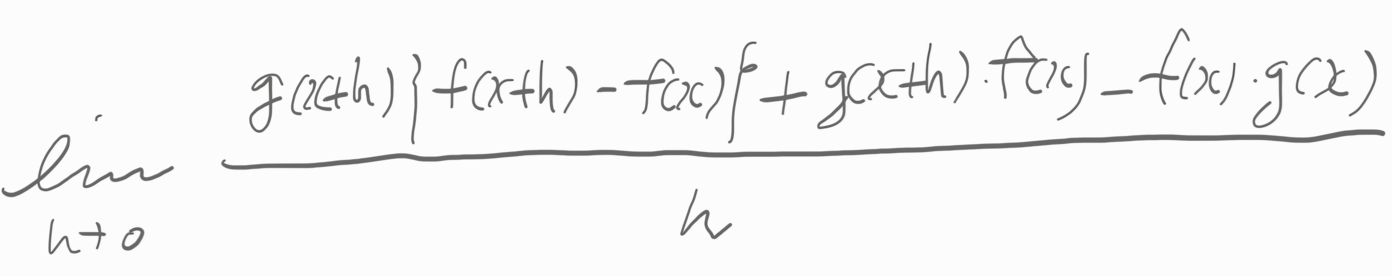
.
.
.

.
.
.
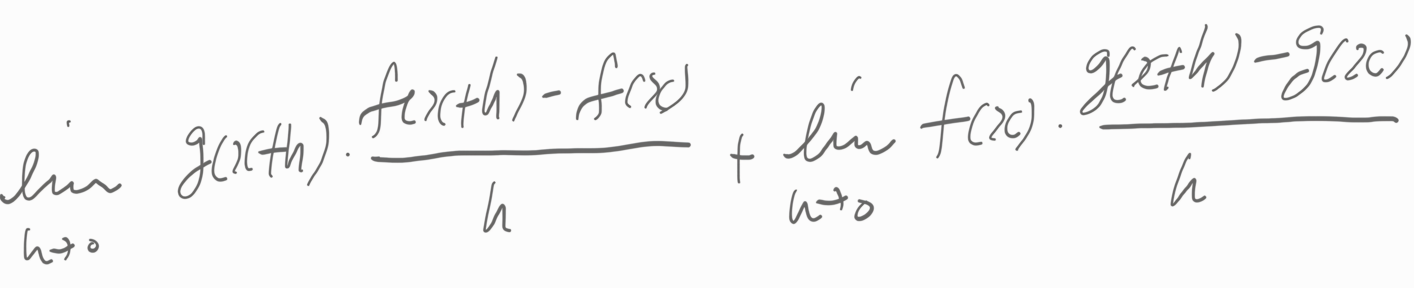
.
.
.
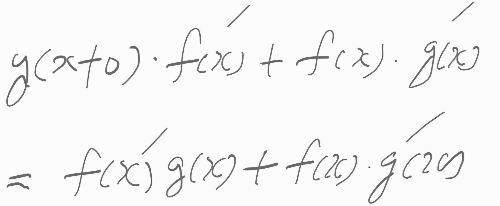
거의 정리가 되었습니다.

이제 곱으로 표현된 함수의 미분을 조금 더 쉽게 풀 수 있습니다.
이미 답을 구했지만, 지금 정리한 미분방법으로 다시 풀어봅니다.

.
.
.
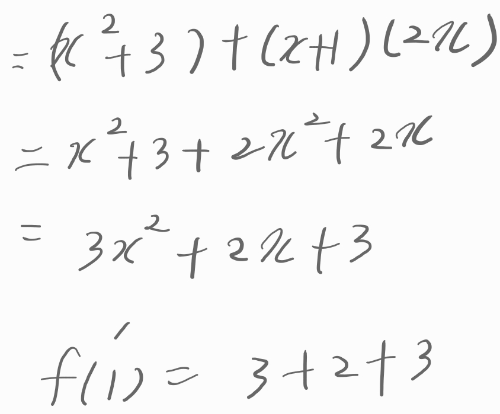
식을 전개해서 풀었던 때랑 결과가 같습니다.
오늘은... 여기까지.
'math' 카테고리의 다른 글
| 두 각의 합과 사인함수 (0) | 2024.12.05 |
|---|---|
| 24학년도 수학18번 (1) | 2024.12.03 |
| 24학년도 수학16번 (1) | 2024.11.29 |
| 24학년도 수학15번 (1) | 2024.11.28 |
| 24학년도 수학14번 (2) | 2024.11.27 |