
최고차항의 계수가 1인 삼차함수 f(x)는
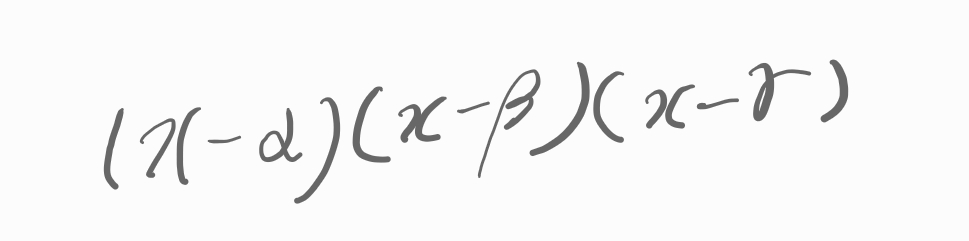
이런 모습이 될 겁니다.
그림을 그려보면,

대충 이런 모습이 될 것 같습니다.
그리고
f(k-1) × f(k+1) < 0를 만족하는 정수 k가 존재하지 않는다는 조건은,
k가 정수이면
f(k-1) × f(k+1)가 0보다 크거나 같다는 말과 같습니다.
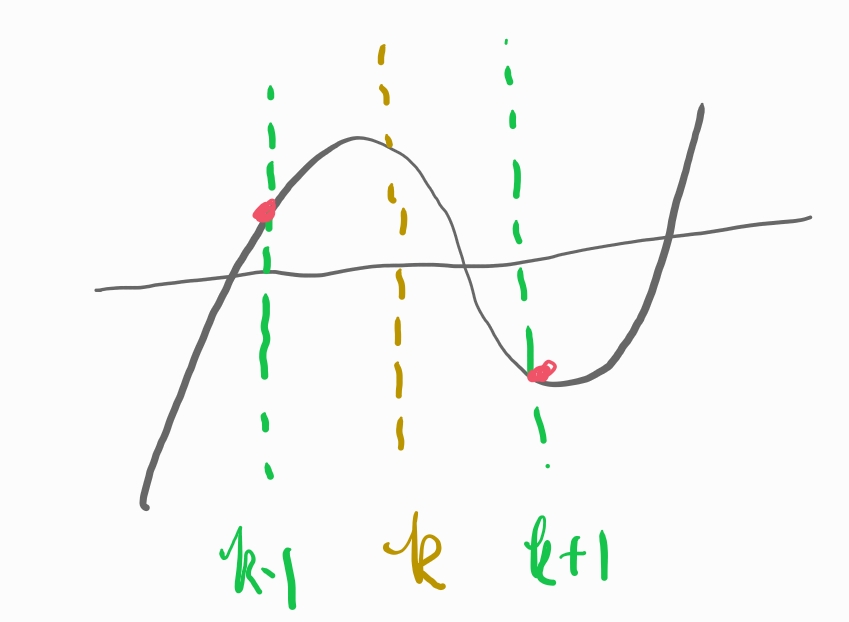
임의의 정수 k를 가정해 보았을 때
f(k-1)의 값과 f(k+1)의 값이 서로 다른 부호를 가지면 조건을 만족할 수 없습니다.
위의 조건을 만족하려면
f(k-1) 또는 f(k+1)이 0이거나
둘 다 음수이거나 둘 다 양수이어야 합니다.

위 조건을 만족하려면
x가 정수일 때 f(x)의 값이 0 이면 될 것 같습니다.
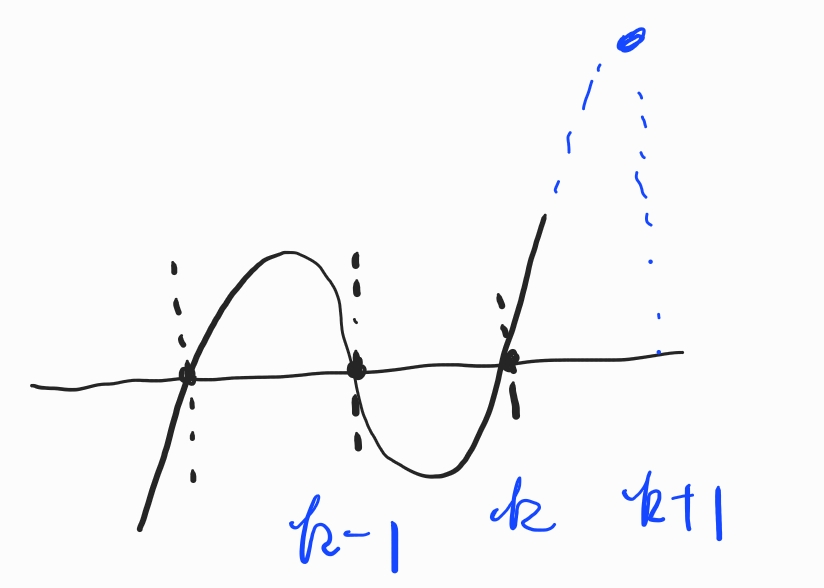
이경우에도 조건을 만족합니다.
만약 k+1을 k라고 가정하더라도
f(k-1) × f(k+1) = 0이므로
조건을 만족합니다.

k가 양의방향으로 1씩 이동하더라도
f(k-1)와 f(k+1)은 모두 양의 값을 갖게 되니 조건을 만족하게 됩니다.

음의 방향도 마찬가지로 조건을 만족합니다.
종합해 보면 f(x)가 x축과 만나는 x는 모두 정수가 되면 될 것 같습니다.
이제 다른 조건을 살펴봅니다.
x가 -1/4일 때의 기울기가 -1/4이라고 합니다.
그리고 x가 1/4일 때의 기울기가 0보다 작다고 합니다.

최고차항의 계수가 양수인 삼차함수에서
기울기가 음수인 영역은 위 그림처럼 극대와 극소의 사이에서 존재합니다.
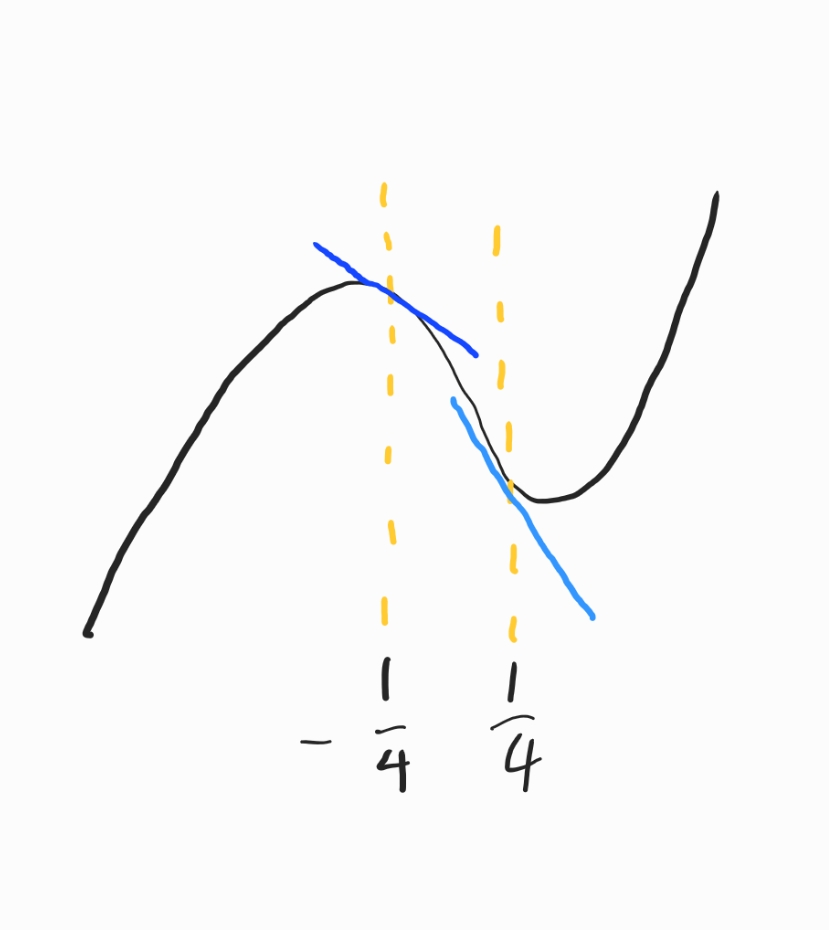
문제의 조건을 그래프에 표시해 보니
x가 0인 지점을 알 수 있을 것 같습니다.

이제 함수 f(x)를 구한 것 같습니다.
x(x-1)(x+1)
그렇다면 구해야 할 f(8)은?
7 ×8 ×9일까요??
뭔가 이상하다는 생각을 지울 수 없습니다.
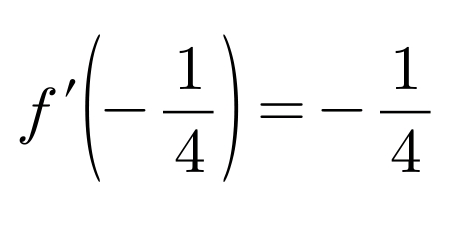
x가 -1/4일 때의 기울기가 1/4인지 검산을 해봅니다.
x(x-1)(x+1) = x(x²-1) = x³-x
f(x)를 미분해 보면
3x²-1이고
이 도함수(미분함수)에 -1/4를
대입해 보니 대충 계산해도 -1/4는 나오지 않습니다.
??
.
.
.
다시 생각을 해보니
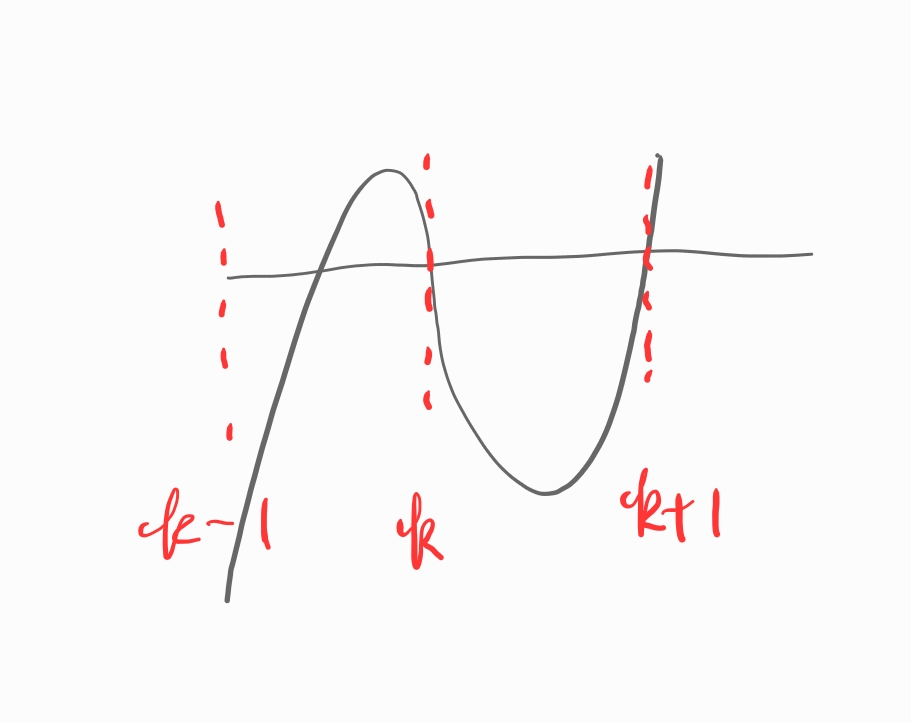
이런 경우도 문제의 조건을 만족합니다.
반드시 f(x)가 x축과 만나는 점의 x값이 모두 정수일 필요는 없었습니다.
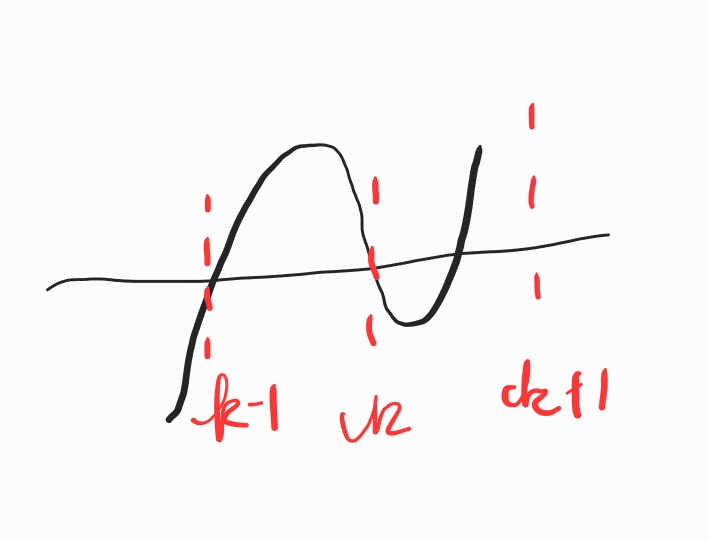
마찬가지로 이런 경우도 조건을 만족합니다.
그런데 생각해 보니,
기울기가 -1/4라면 극값에 가까운 값일 테고
0 이 -1/4과 1/4이라는 좁은 범위에 있는 경우라면,
x가 -1/4인 기울기가 -1/4인 점은 극대에 가까운 점이라고 보는 게 타당합니다.
다시 함수 f(x)를 그려보면
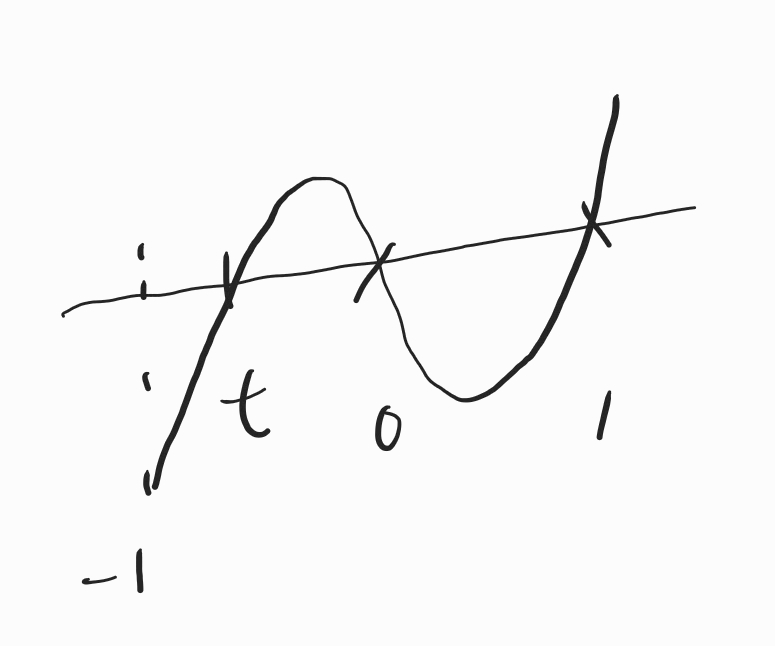
이런 모양이 되겠네요.
그래서 함수 f(x)는

입니다.
이 함수의 도함수는

입니다.
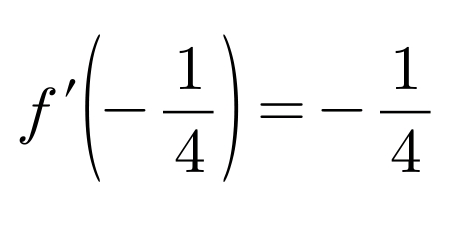
이 조건을 통해서 f(x)가 x축과 만나는 점 t를 구할 수 있습니다.
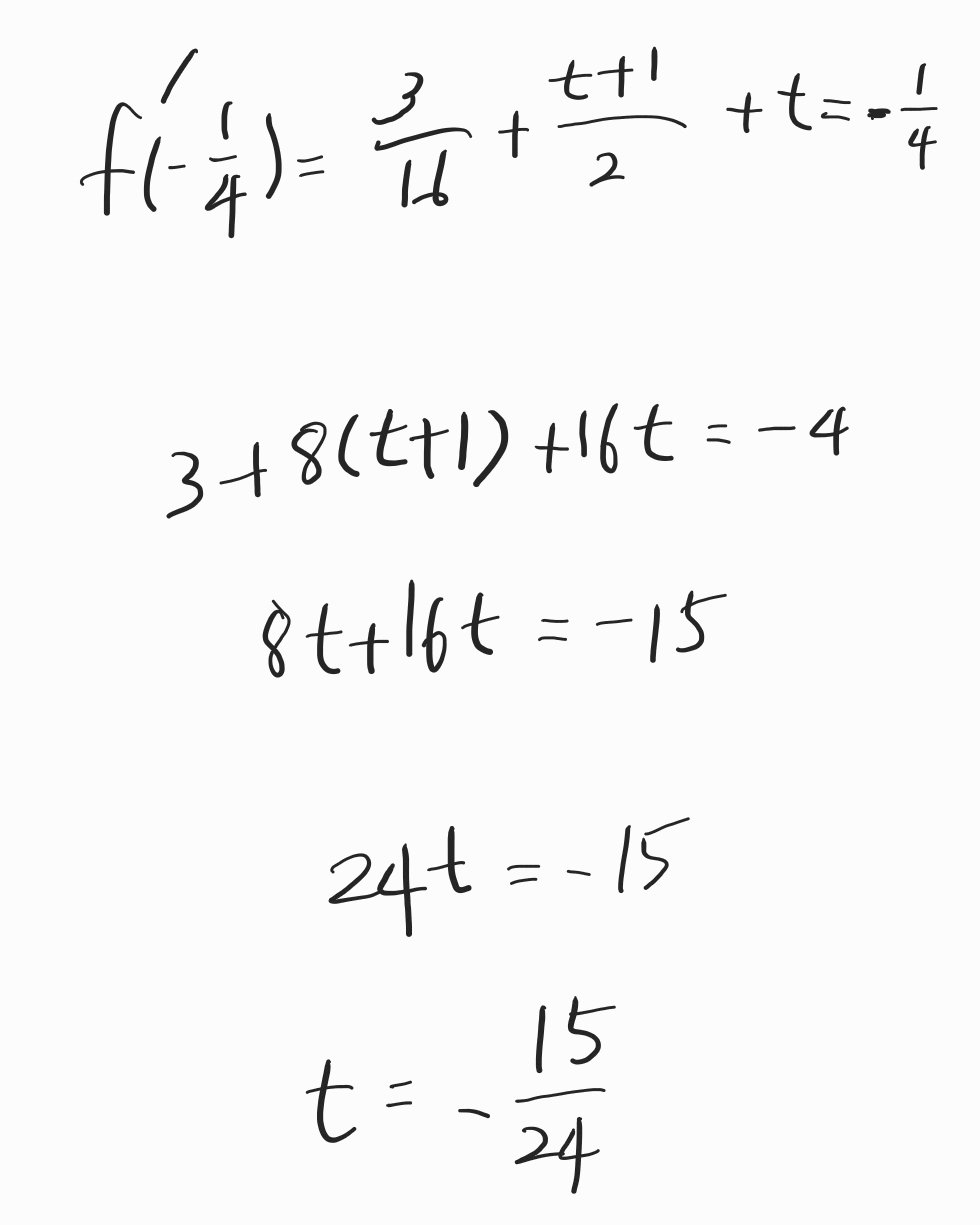
이제 함수 f(x)를 알 수 있습니다.
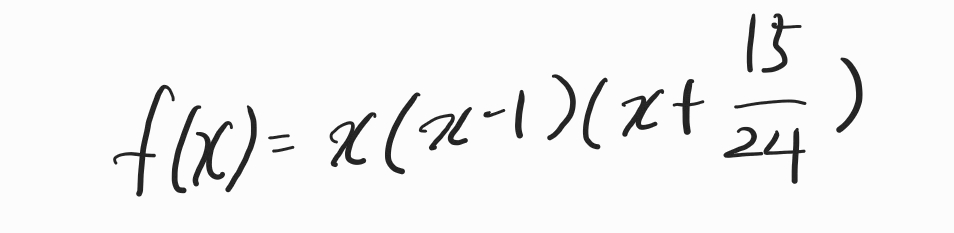
그리고 f(8)도 구할 수 있습니다.
8 ×7 ×(8+15/24)
끝.
'math' 카테고리의 다른 글
| 24학년도 확률과 통계 24번 (0) | 2025.01.13 |
|---|---|
| 24학년도 확률과 통계 23번 (0) | 2025.01.13 |
| 24학년도 수학21번 (0) | 2024.12.30 |
| 24학년도 수학20번 (1) | 2024.12.21 |
| 어떤 직선과 수직인 직선(1차 함수)의 기울기 (1) | 2024.12.09 |