
21번 문제입니다.
이쯤 되니 스스로의 국어실력이 의심됩니다.
문제가 무슨 말인지 이해하기 어렵습니다.
문제의 상황을 이해하기 위해서
함수 f(x)를 그려봐야겠습니다.
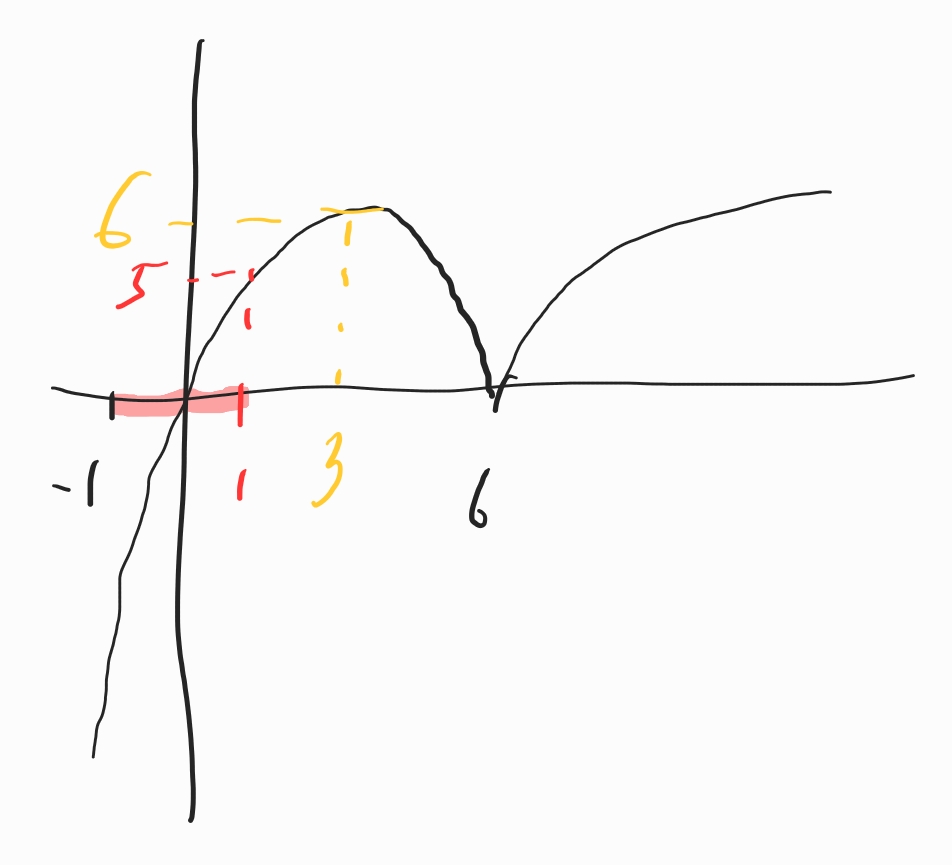
x가 -1 이상이고 6 미만 일 때
f(x)는
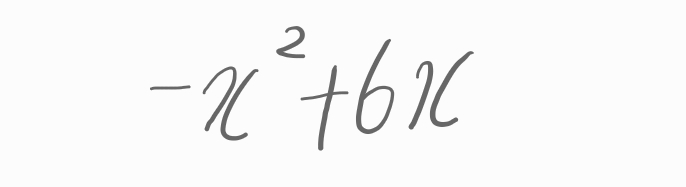
입니다.
인수분해를 하면,
-x(x-6)입니다.
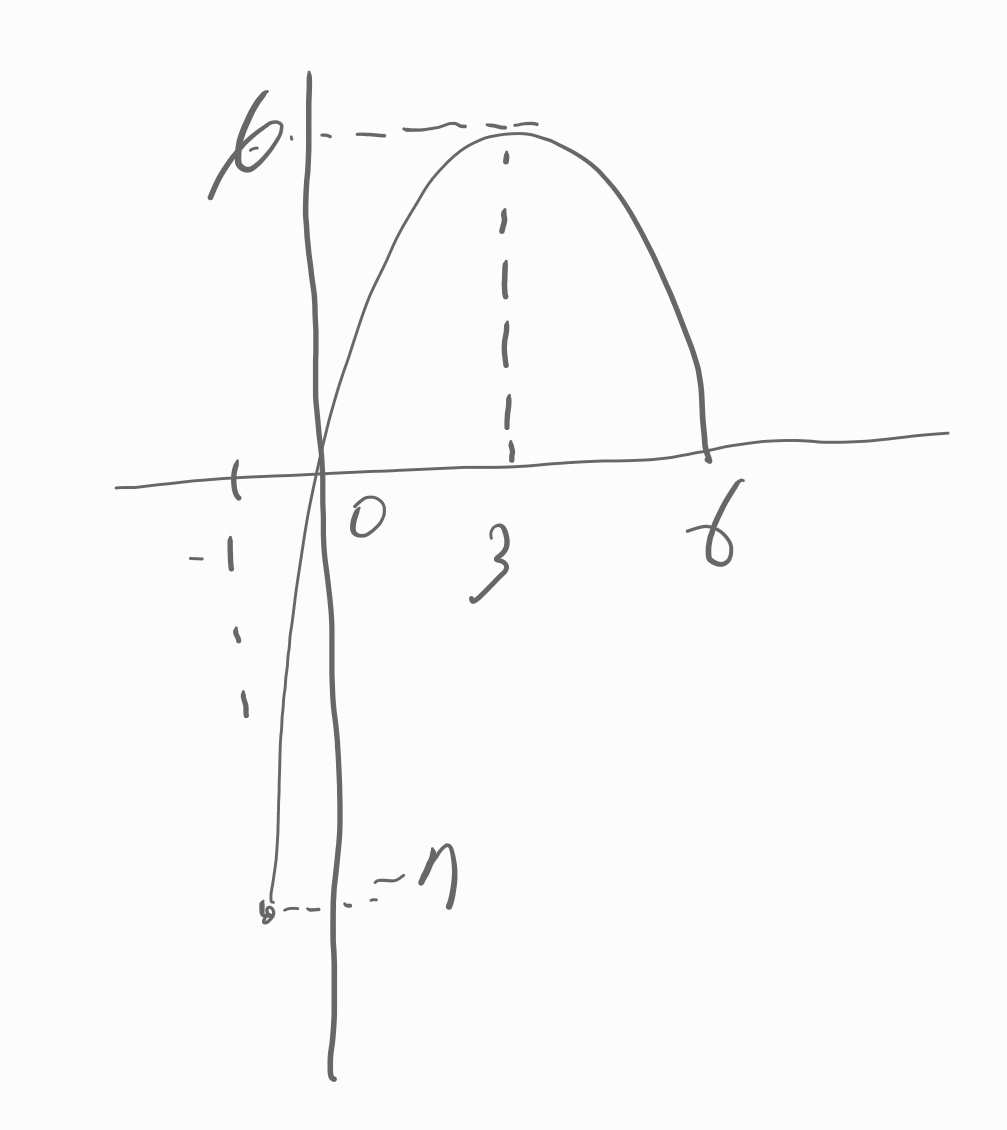
이 함수는 x가 0과 6일 때 x축과 만납니다.
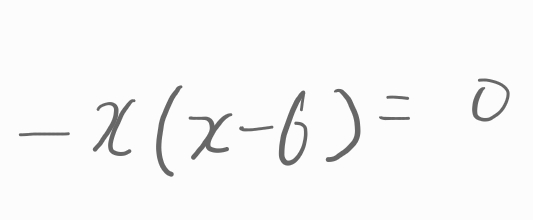
x가 -1일 때 f(x)는 -7입니다.
f(x)의 극대값은 접선의 기울기가 0 이 되는,
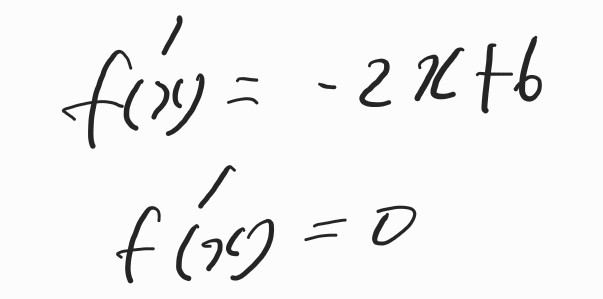
x가 3일 때의 f(x) 값입니다.
계산해 보면 6입니다.
f(3)=6
[2차 함수에서 극대나 극소는 함수의 대칭축에서 만들어지기 때문에 x값 0과 6의 중간을 찾으면 극대나 극소의 x값을 구할 수 있습니다.]
이제 x의 범위가 -1보다 크거나 같고 6보다 작을 때의 함수 f(x)를 그려 볼 수 있습니다.
다음으로 x의 범위가 6보다 크거나 같을 때
f(x),
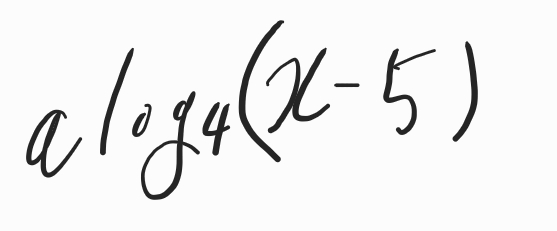
는
로그함수

를 x축 방향으로 5만큼 이동한 함수입니다.
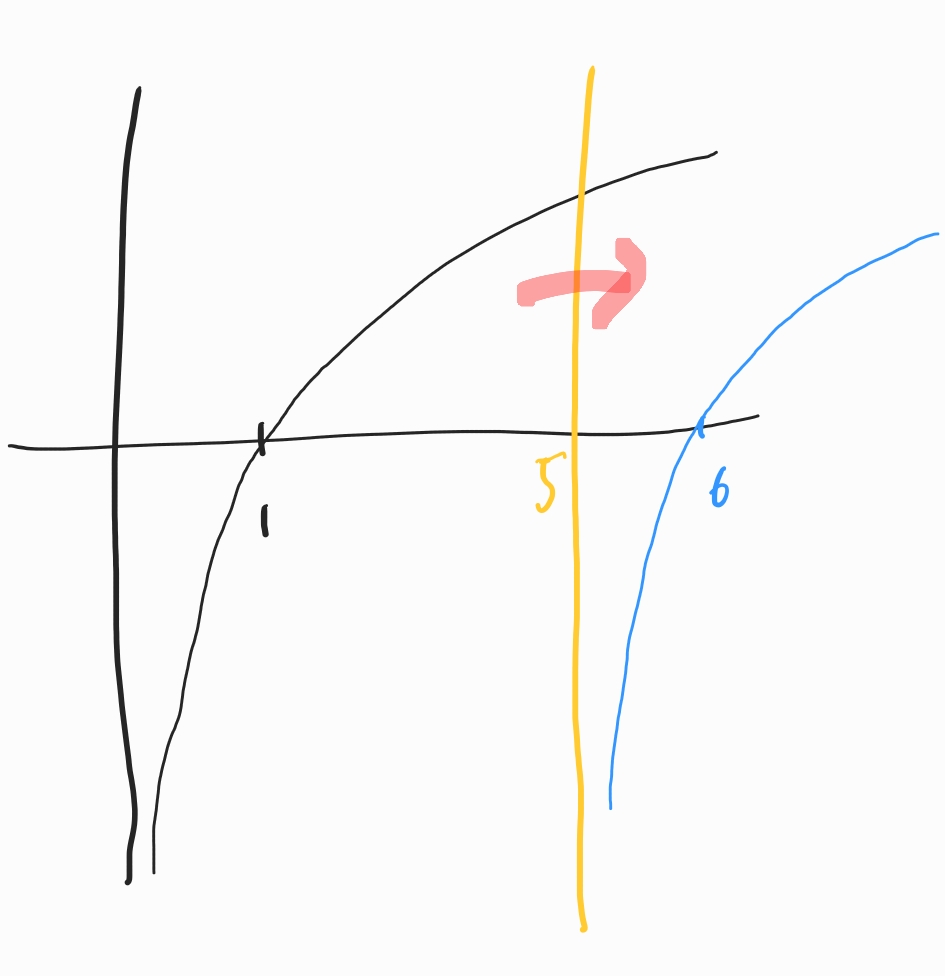
이제 x가 -1보다 크거나 같은 범위에서의 함수 f(x)를 그려볼 수 있습니다.
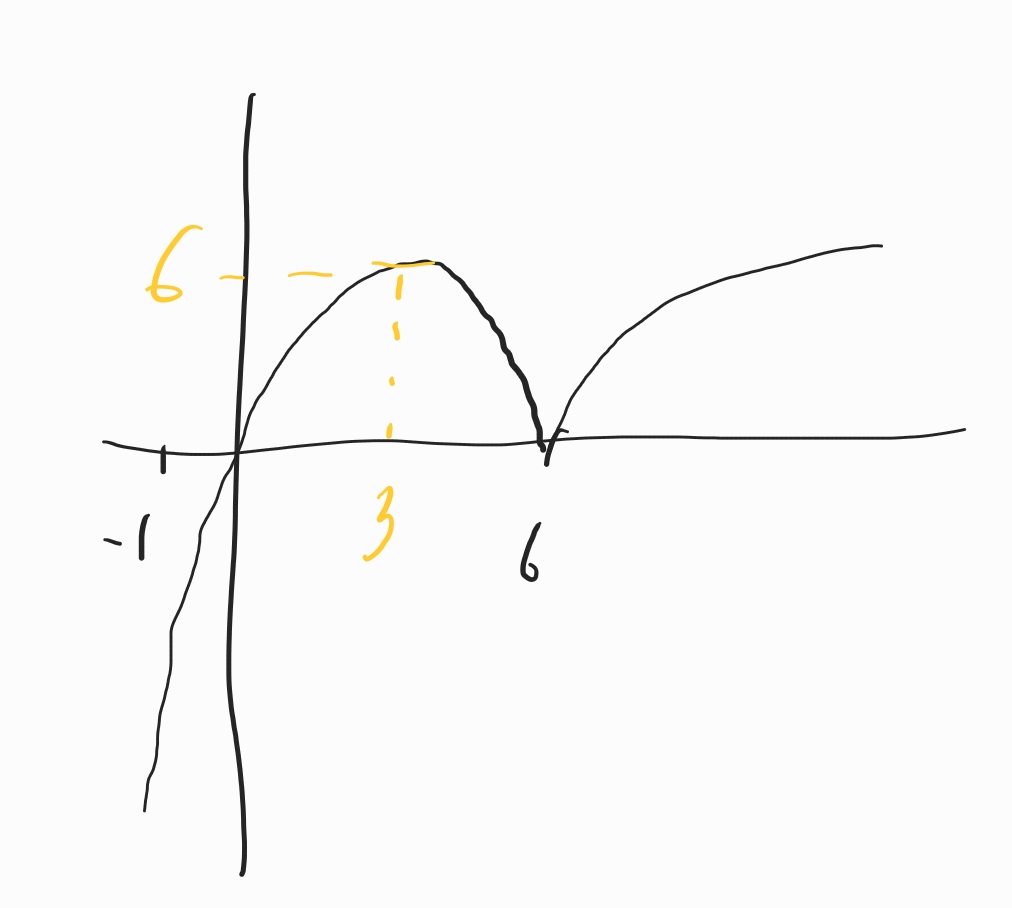
대충 이런 모습이 됩니다.
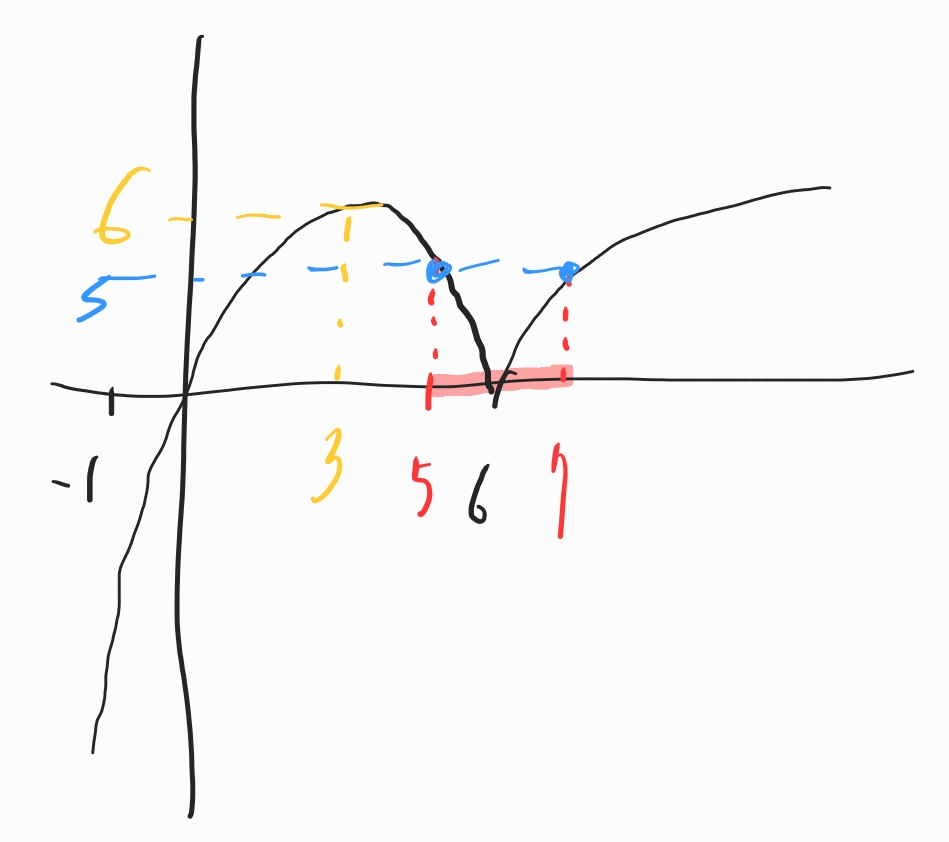
이런 상황에서 t가 0보다 크거나 같을 때
닫힌구간 [t-1, t+1]에서 최댓값 g(t)가
최소 5 이상이 되는 a를 찾아야 합니다.
t=0이라면
닫힌구간 [-1,1]에서 최댓값 g(t)는
f(1) 값이 됩니다.
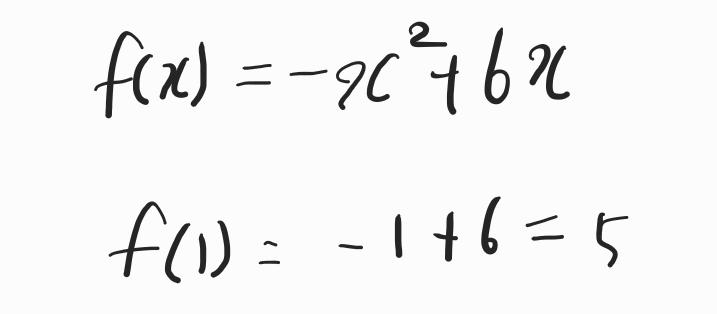
5입니다.
t=6이라면
닫힌구간은 [5,7]이고
2차 함수인 f(5)의 값은
-5² + 6 ×5 = 5 이어서
t가 6이 될 때까지 g(t)는 5 이상이 됩니다.
그런데 t가 6을 초과하는 순간이
(닫힌구간이 7을 초과하는 순간이)
g(t)의 최솟값이 5이어야 한다는 문제의 조건을 만족하려면
f(7)는 5이어야 합니다.
그래서
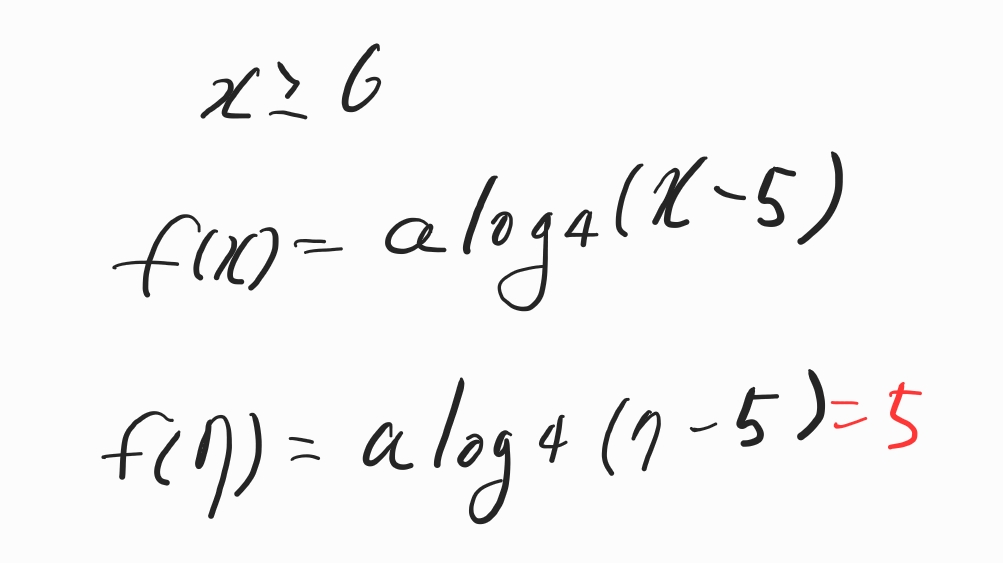
.
.
.
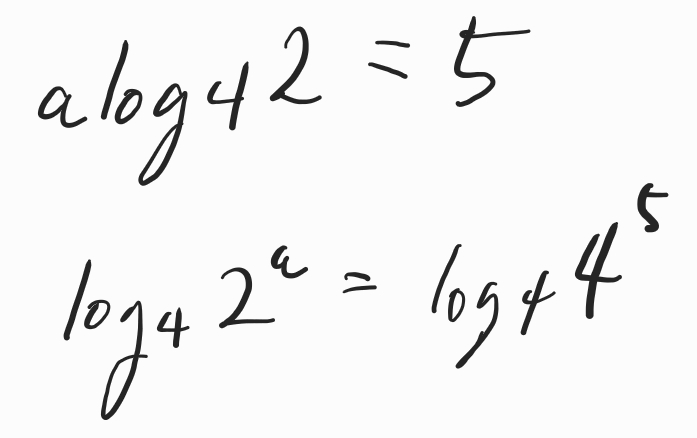
2 ª 가 4의 5 제곱과 같아야 합니다.
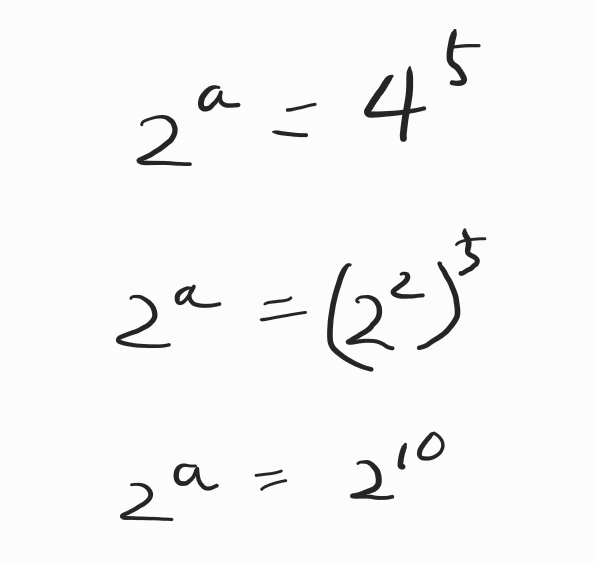
문제의 조건을 만족하는 a를 구했습니다.
'math' 카테고리의 다른 글
| 24학년도 확률과 통계 23번 (0) | 2025.01.13 |
|---|---|
| 24학년도 수학22번 (0) | 2025.01.10 |
| 24학년도 수학20번 (1) | 2024.12.21 |
| 어떤 직선과 수직인 직선(1차 함수)의 기울기 (1) | 2024.12.09 |
| 24학년도 수학19번 (0) | 2024.12.06 |