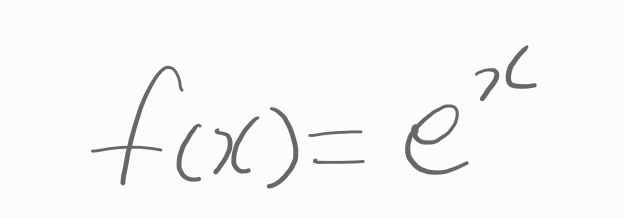x가 2일 때의 함수의 미분값을 구하는 문제입니다.함수의 미분에 대한 지난번 글을 링크해 봅니다.{도함수(미분) 관련 링크}https://blogger3036.tistory.com/m/18 24학년도 수학2번24학년도 수학 두 번째 문제를 풀어보려고 합니다.오블완 챌린지 덕분에 팔자에 없는 수학 공부를 합니다. 아... 그냥 미분문제구나 싶습니다.단. 순. 한.? f(x) 함수에서 x가 2일 때 미분값이라blog.urno.co.kr결국, f(2)'의 값을 찾는 문제입니다.함수 f(x) = x³-8x+7의 도함수는f(x)'=3 x² - 8입니다.x에 2를 넣어서 풀면3 ×2² - 8계산하면 문제의 답을 구할 수 있습니다.끝.