어떤 직선과 수직인 직선(1차 함수)의 기울기

좌표평면에서
1차 함수 y = ax에서 x의 계수 a는
x의 증가량분의 y의 증가량을 나타냅니다.
만약, y = 2x라는 함수를 가정한다면,
이 함수는 x가 1 증가할 때, y는 2 증가합니다.
다시 말하면, x의 계수 a는 직선(1차 함수)의 기울기를 의미합니다.
 
그렇다면, 함수 y = ax와 직각으로 만나는 직선은 어떻게 찾을까요?

 
y = ax와 수직인(직각으로 만나는) 직선 y = bx + c를 가정해 봅니다.

우선, 상수 c는 x가 0일 때, y축과 직선 y = bx + c이 만나는 점입니다.
그리고 b는 직선 y = bx + c의 x의 계수로 기울기입니다.
 
이 기울기 b를 어떻게 구할 수 있을까요??
.
.
.

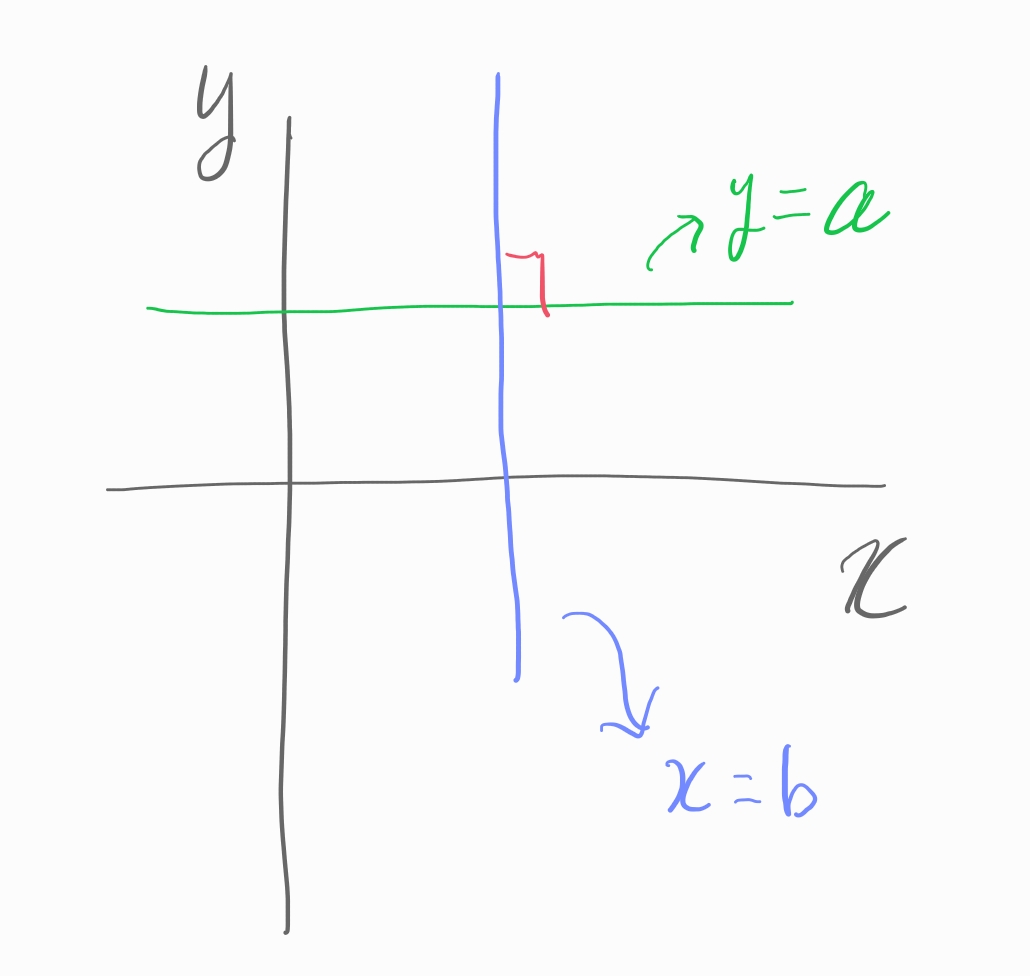
x축에 평행한 직선과
y축에 평행한 직선은 서로 수직으로 만납니다.
이 함수들은 서로 x와 y를 바꾼 것처럼 보입니다.

x와 y를 서로 바꾼다는 것은 원점을 기준으로 좌표평면을 90도 돌린다는 말과 같습니다.

좌표평면을 90도 돌리면,
y축은 x축이 되고
x축은 y축이 됩니다.
그리고 직선도 90도 돌아갑니다.

처음 가정했던 직선과 90도 돌아간 직선의
기울기가 같다는 것이 눈으로 확인이 되네요.

정리해 보면,
어떤 직선과 직각으로 만나는 직선의 기울기는,
함수식에서 x와 y를 자리 바꿔서 구할 수 있습니다.

y = ax
x = ay
y = (1/a) x

끝.