24학년도 수학12번

f(x) 함수는 3차 함수입니다.

대충 그려봅니다.
f(x)가 0이 되는 점들이 우선 눈에 보이네요.

내친김에 극대점을 찾아봅니다.
t가 0과 6 사이의 실수라고 했기 때문에
x가 6보다 큰 극소점은 신경 쓰지 않겠습니다.

0과 6 사이에 극대가 있다면,
그림으로 봤을 때 아마도 x가 3일 때 일거라 짐작해 봅니다.
혹시 모르니, 확인을 위해서 f(x)를 미분해 봅니다.

이대로는 미분이 어려워서
식을 정리해 봅니다.

미분하기 쉬운 형태가 되었습니다.

x² - 10x + 18 이 0이 되는 x값을 찾아야 하는데
인수분해가 되는 모양이 아닙니다.
x가 정수가 아니었네요.
근의공식을 이용해 계산해 봅니다.

.
.
.

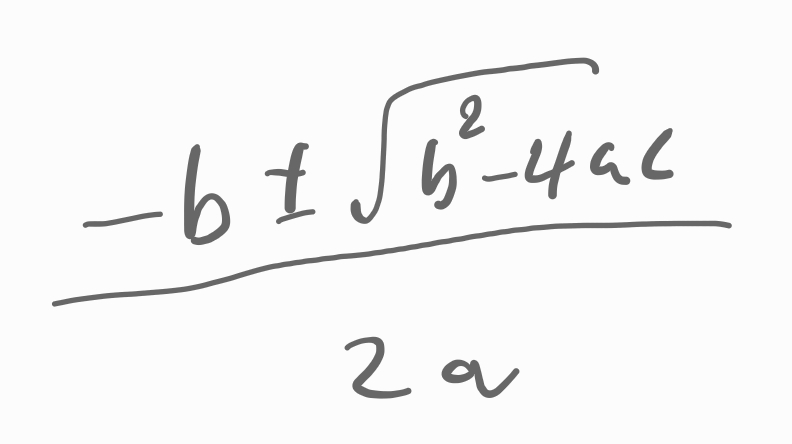
함수 f(x)의 극대는 처음 예상했던 x가 3일 때가 아니었습니다.

 
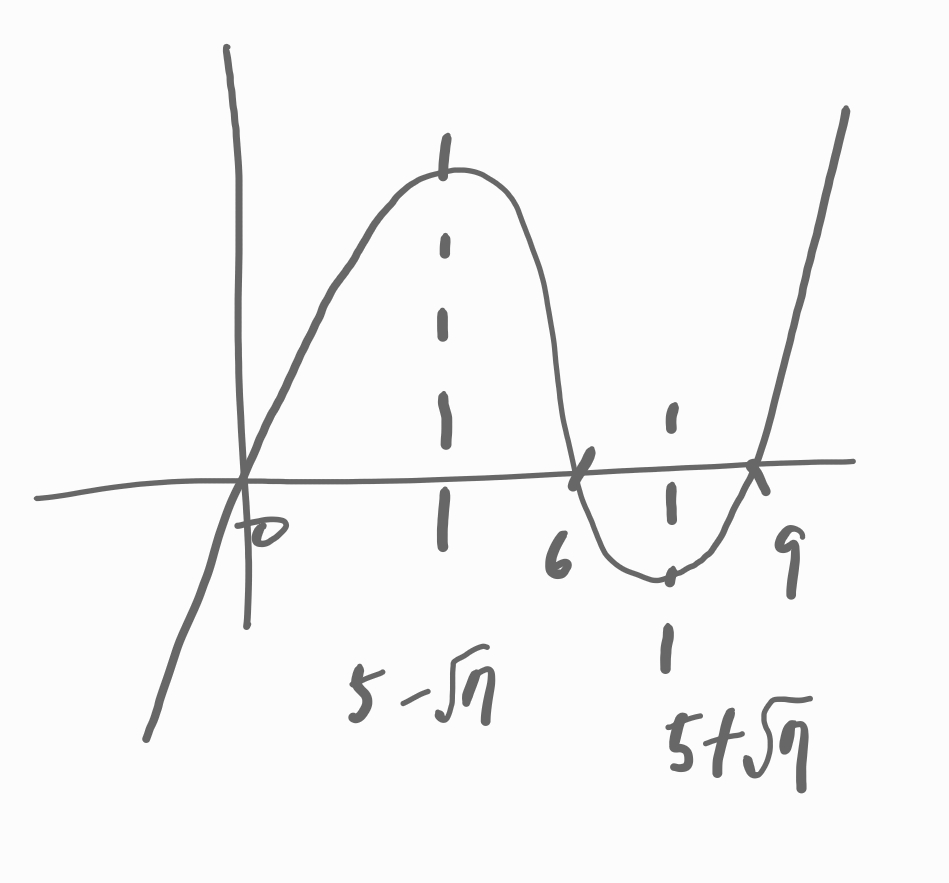
이렇게 되면 다른 풀이방법을 찾아야 할 것 같습니다.
{무리수가 포함된 복잡한 계산도 계산이지만
선지에는 무리수가 없기 때문입니다.}
.
.
.
그래서 문제의 다른 부분을 살펴봅니다.
 
g(x)는 x가 t보다 크거나 같은 경우

라고 했습니다.
찬찬히 들여다보니
- x라는 1차 함수(직선함수)가 보입니다.

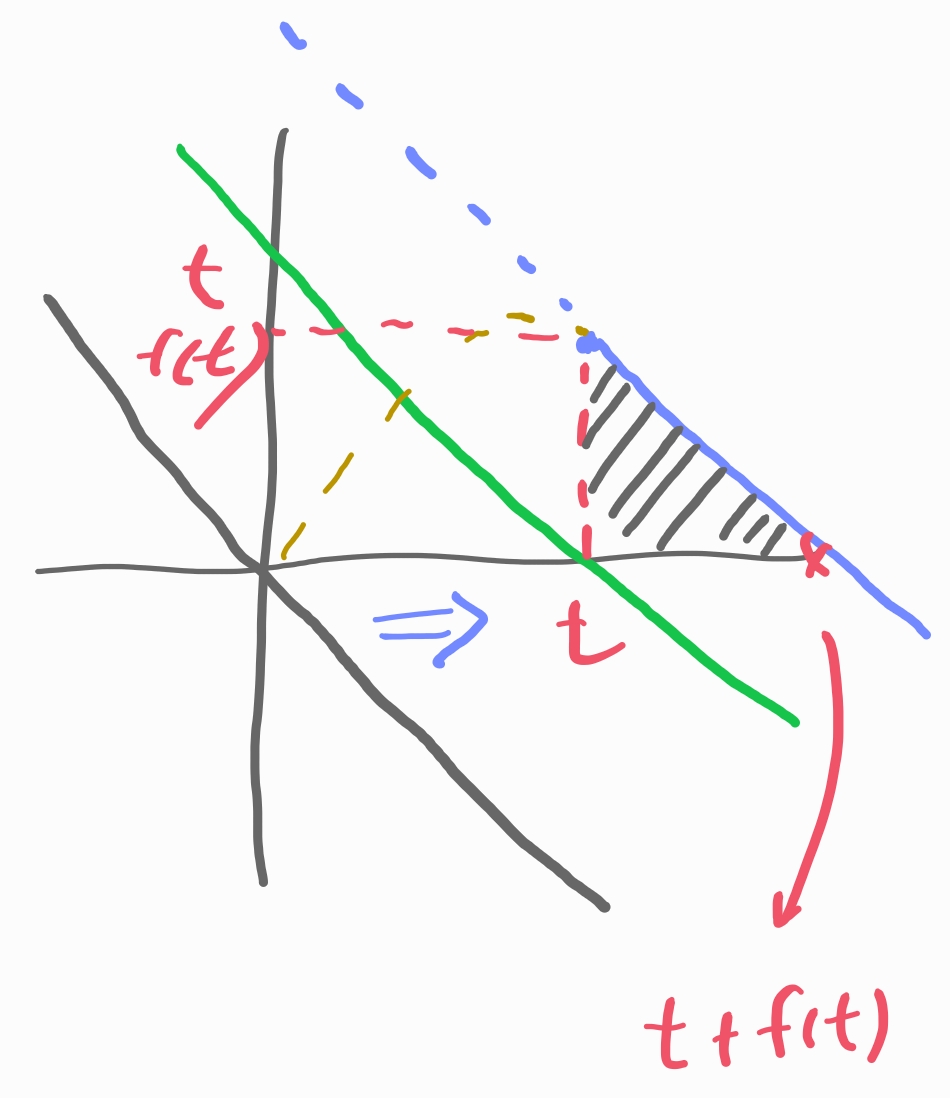
- ( x - t ) + f(t)는
함수 -x를 x축으로 t만큼
y축으로 f(t)만큼 나란히 이동시킨 함수입니다.

다시 정리하면
g(x) 그래프와 x축으로 둘러싸인 영역의 면적은
x가 t보다 작을 때는,
f(x)와 x축으로 둘러싸인 넓이
x가 t보다 크거나 같을 때는,
- ( x - t ) + f(t)와 x축으로 둘러싸인 넓이를 
합한 것입니다.
 
그럼 이제 이 면적을 구해봅니다.
 
x가 t보다 작을 때의 f(x)와 x축으로 둘러싸인 넓이는

입니다.
 
그리고, x가 t보다 크거나 같을 때의 - ( x - t ) + f(t)와 x축으로 둘러싸인 넓이는

입니다.
 
두 개의 식을 정리해서 표현하면,

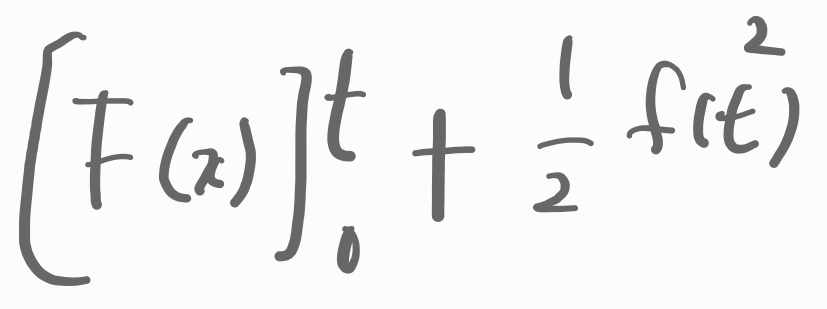
문제에서 구하고자 하는 넓이입니다.
이 넓이를 임의로 h(t)라고 해봅니다.
 
t가 0과 6 사이에서 h(t)는 어떤 형태로든 극대를 가질 거라고 예상해 봅니다.

 
 
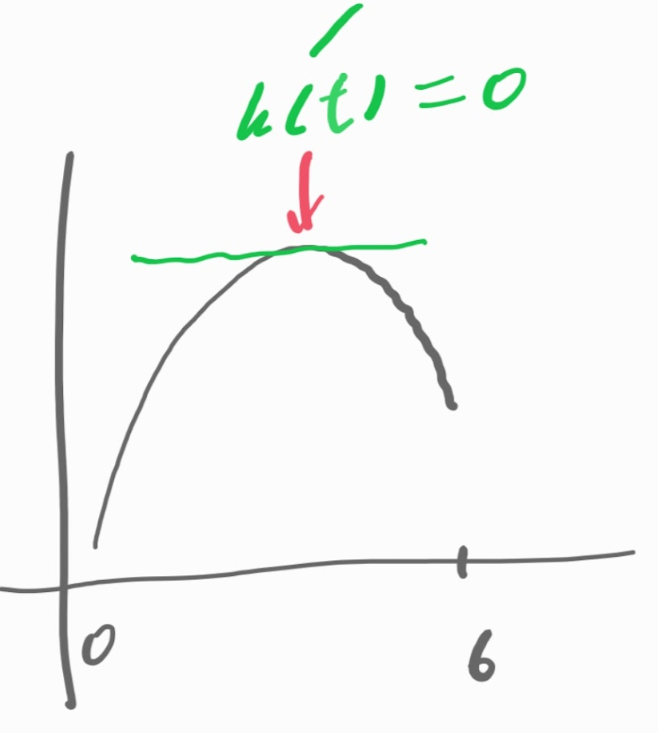
그래서 이 h(t) 함수의 미분함수가 0이 되는 t의 값을 찾아보기로 합니다.
 
h(t)함수를 풀어보면,

이고,
이 함수를 미분하면,

입니다.
 
다행히(?) f(0)은 0입니다.

 
그래서 위 식을 정리해보면

.
.
.

이 값이 0이 되는 t를 찾으면 됩니다.
 
그런데, f(x)는 x가 0, 6, 9일 때 0이 된다고 했었습니다.
그래서 f(t)는 0이 될 수 없습니다.
왜냐하면, t는 0과 6 사이에서만 정의되어 있습니다. 

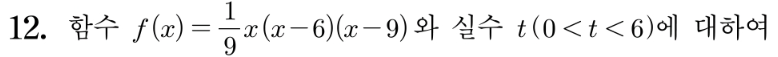
라고 문제에서 그랬지요.
 
그렇다면 h(t)의 미분함수가 0 이 되는지는

여기에서 찾아야 합니다.
f(t)를 미분하면
1/3 (t² - 10t + 18)
여기에 1을 더합니다. 1/3로 묶은 괄호 안으로 1을 넣겠습니다.
{괄호 안에서 + 3}
1/3 ( t² - 10t + 21 )
 
결굴 ( t² - 10t + 21 ) 이 0이 되는 값을 찾으면 됩니다.
인수분해하면,
(t - 3)(t - 7) = 0
 
t가 3이거나 7이면 0 이 됩니다.
다시 말해서 h(t) 함수는 t가 3이거나 7일 때 극값을 갖습니다.
0 < t < 6이라고 했기 때문에,
이문제에서 찾으려던 넓이는 t가 3일 때, 최대가 됩니다.
 
이제 최대 넓이를 구해봅니다.
 
t 대신 3을 대입해서 풀어봅니다.

먼저 앞부분을 적분해서 구해봅니다.

.
.
.

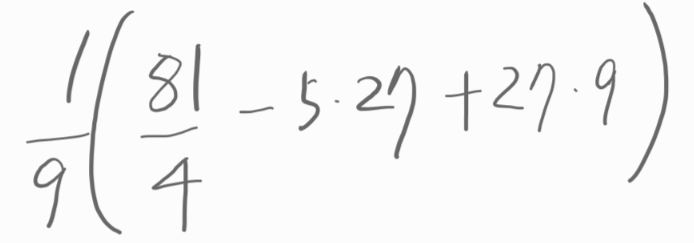
{복잡한 계산을 하고 있으니.... 현타가 옵니다만 참고 계산합니다.}

.
.
.
4분의 57이라는 값을 얻었습니다.
 
이제
삼각형의 넓이를 구해봅니다.
f(3) = 6입니다.
.
.
.
{잠시 생각에 잠깁니다.}
{처음에 잘 못 생각해서 찍었던, x의 값이 떠오릅니다.}
{그렇습니다. 3이었습니다.}
{그냥 모르고 풀었더라면... }
{그래도 답은 맞았던 것이었습니다...}
 
어쨌든, f(3)이 6이라면, 삼각형의 넓이는 18입니다.

 
이제 두 값을 더하면 끝.