24학년도 수학10번

수직선 위를 움직이는 두 점...
먼저 P점의 속도와 움직이는 모양을 살펴봅니다.

속도를 나타내는 함수가 2차 함수입니다.
그림을 대충이라도 그려보기 위해서 인수분해를 해보면,

점 P는 1초와 5초에서 속도가 0이네요.

그리고 1초까지는 속도가 양수,
1초일 때 속도가 0.
1초에서 5초까지는 속도가 음수,
5초일 때 속도가 0.
5초부터는 다시 속도가 양수입니다.

수직선 위를 움직이는 점이니
이런 식으로 움직이겠네요.
점 Q의 속도를 나타내는 함수는 1차 함수입니다.

그래프를 그려봅니다.

3.5초까지 속도가 음수,
3.5초의 속도가 0
그 이후로는 속도가 양수입니다.
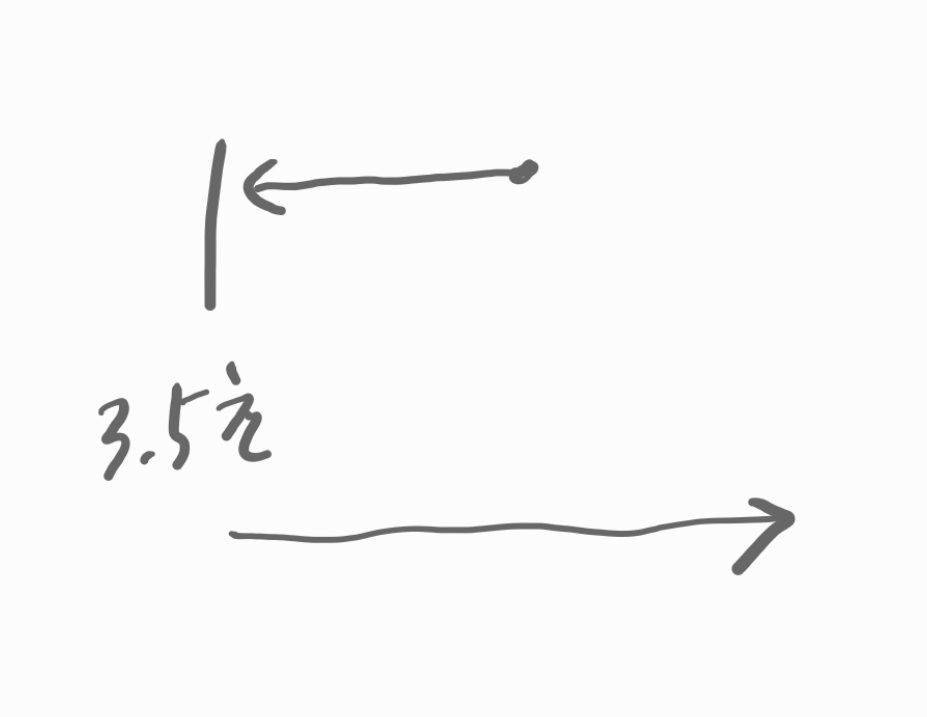
대충 이런 식으로 움직입니다.
두 점의 속도를 하나의 평면에 그려보면,
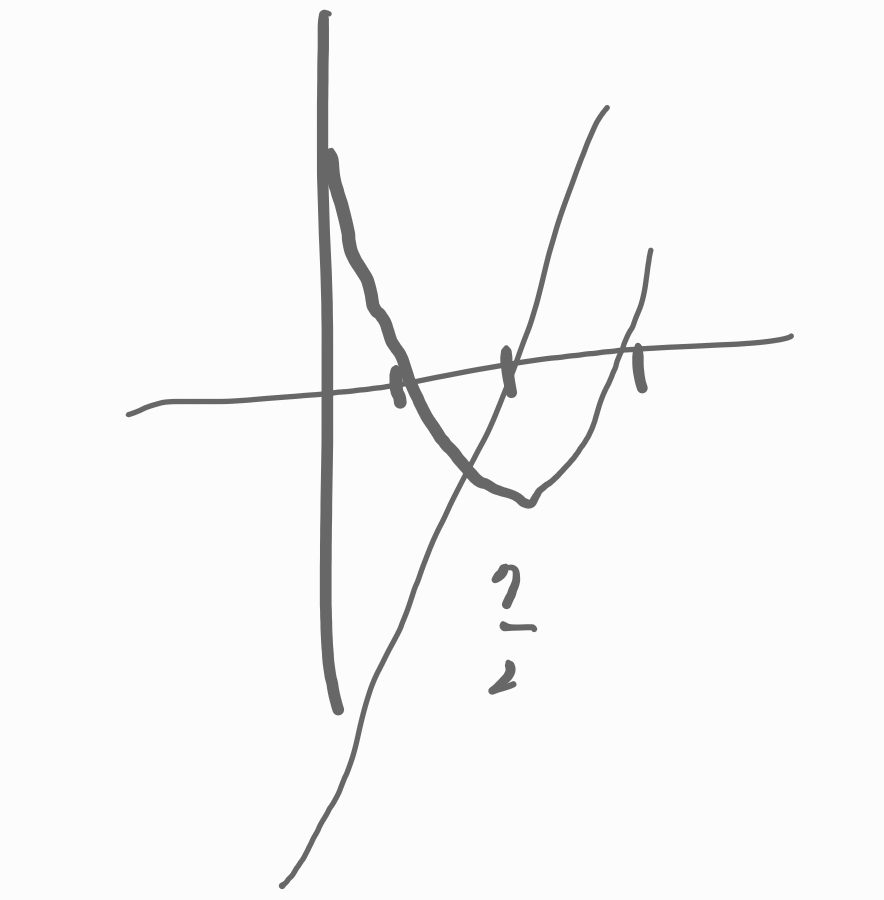
대충... 대. 충. 이런 모양입니다.
.
.
.
그런데 두 점사이의 거리는 변위(움직인 거리)의 차이입니다.
움직인 거리를 미분하면 속도가 나옵니다.
반대로 속도를 적분하면 변위가 나옵니다.
그래서 각 점의 속도를 적분해서 그 차이로 두 점 사이의 거리를 구해볼까 합니다.
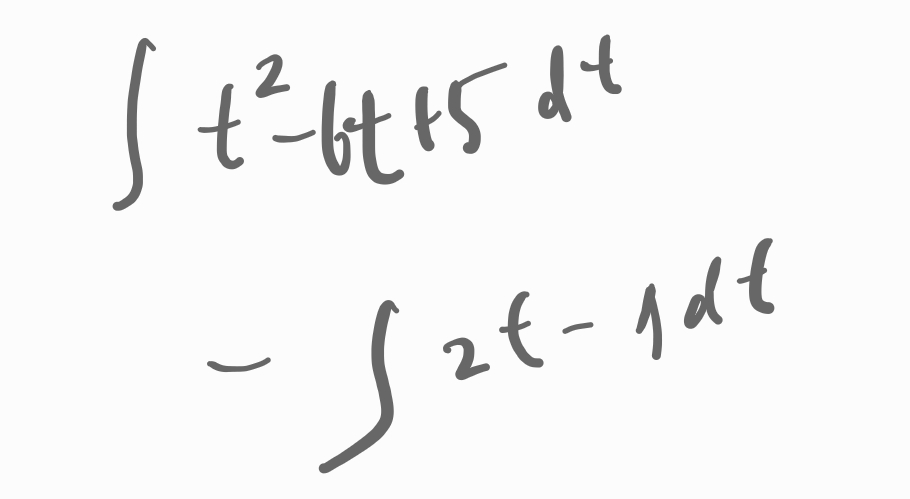
.
.
.
부정적분을 해봅니다.
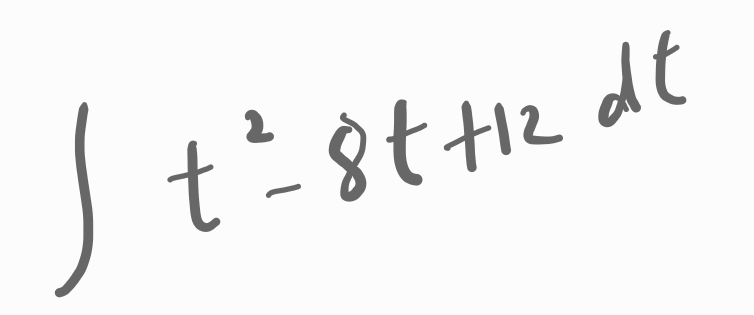
문제에서는 두 점 사이의 거리를
f(t)라고 했습니다.
그럼 f(t)는,
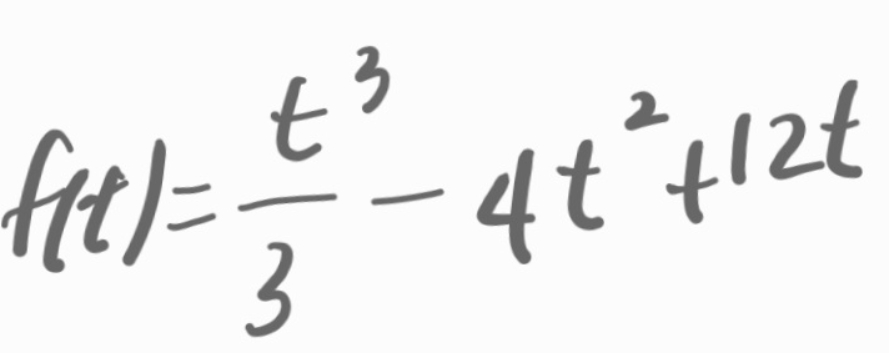
입니다.
사실, 부정적분을 하면
상수항을 생각해야 합니다.

상수항의 미분값은 0 이기 때문에 적분할 때 상수항 C를 염두해둬야 합니다.
이 문제에서 t는 0 보다 크거나 같다고 했습니다.
그리고 t기 0 일 때 동시에 원점에서 출발한다고 했으니
t = 0 일 때 두 점사이의 거리도 0입니다.
그래서 상수항 C는 0입니다.
결국,
f(t)는
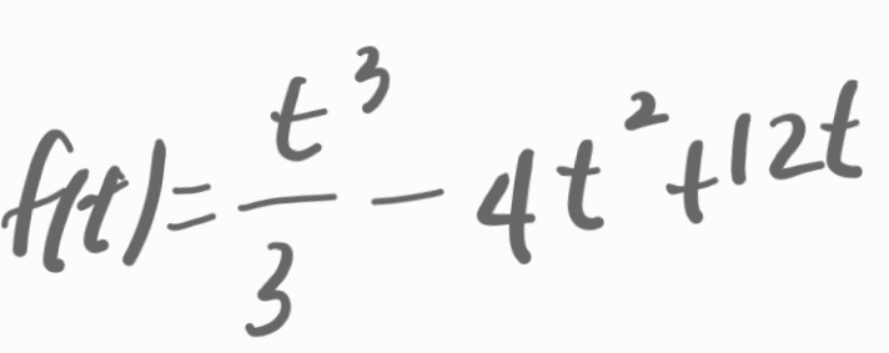
이네요.
이 함수를 다시 정리해 보면,
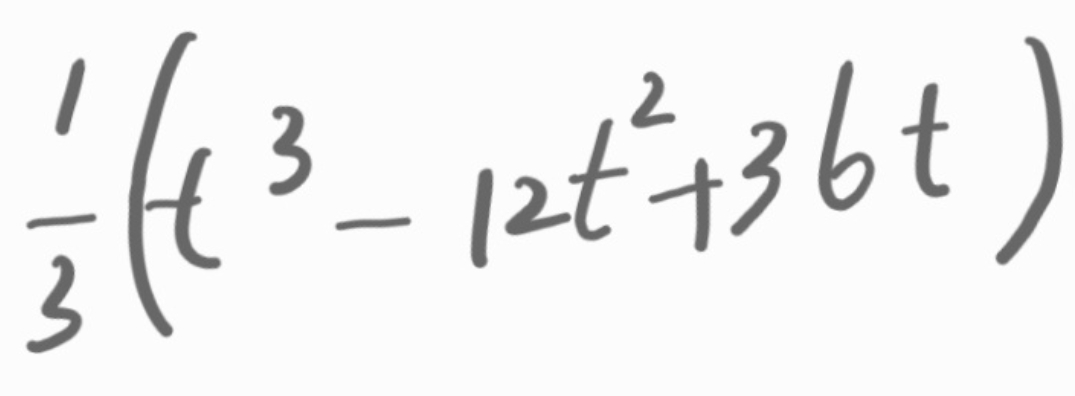
.
.
.
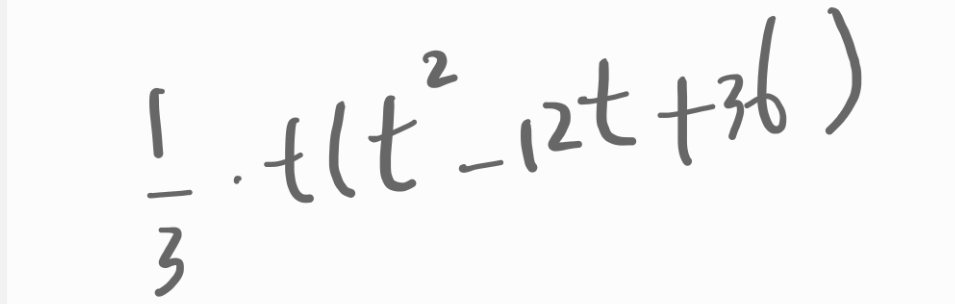
조금 더 정리 해봅니다.
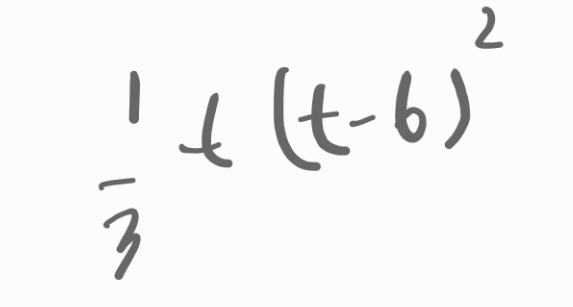
그림을 그려봅니다.
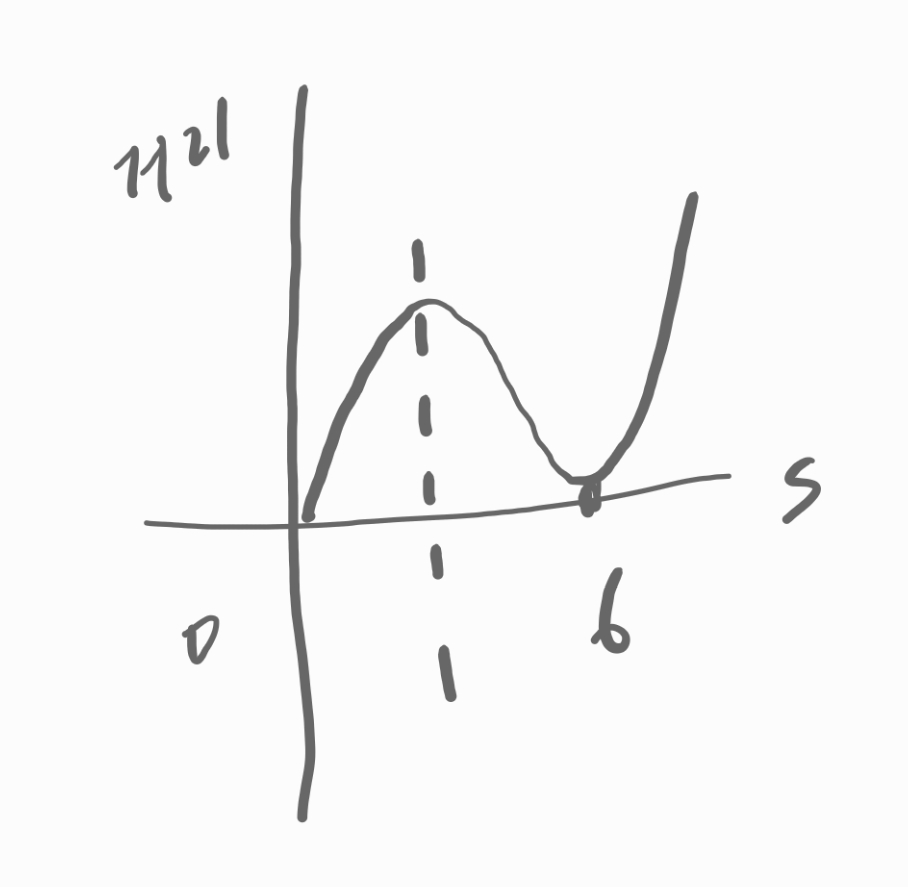
0초 이후, 두 점 P와 Q사이의 거리는
늘었다가,
극대점에서 속도가 0이었다가 줄어듭니다.
이후 극소점 6초에서 속도가 0이 되었다가 다시 늘어납니다.
극소점의 시간은 이미 알게 되었지만,
극대점에서의 시간 t를 알기 위해서 f(t) 함수를 미분해 봅니다.
미분값이 0 인 t를 구하면 됩니다.
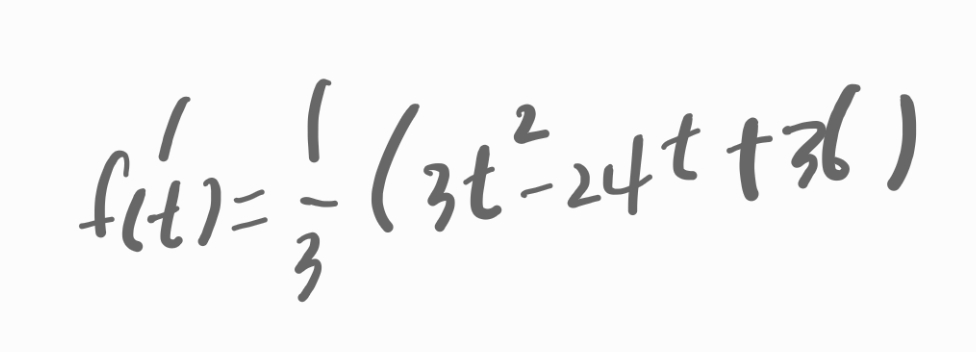
.
.
.
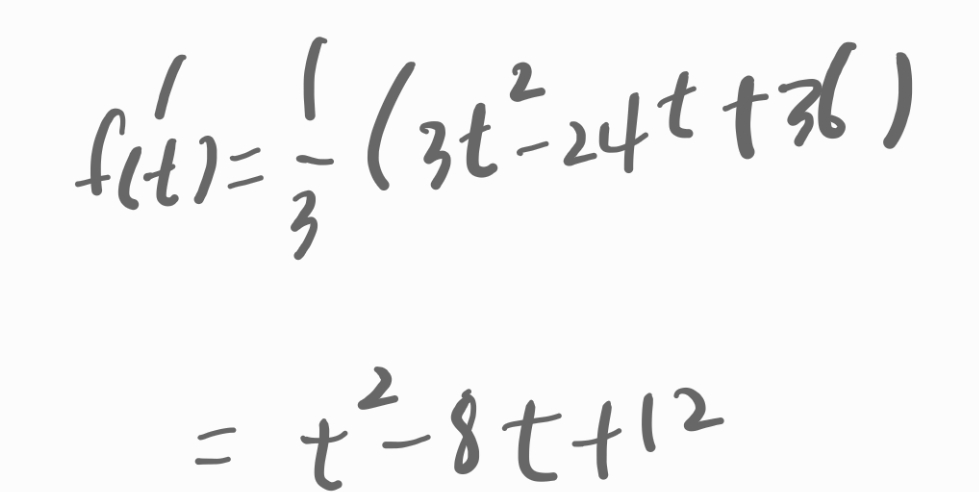
인수분해 해봅니다.
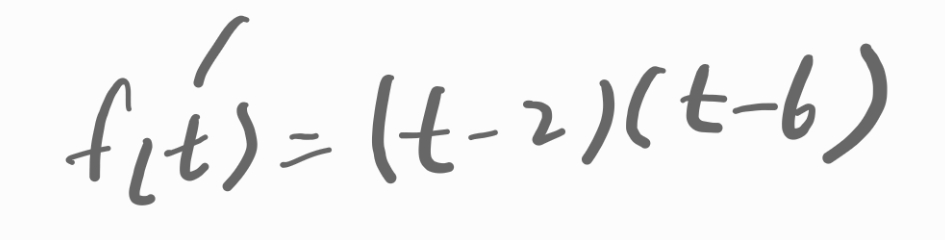
2초와 6초에서 속도가 0입니다.
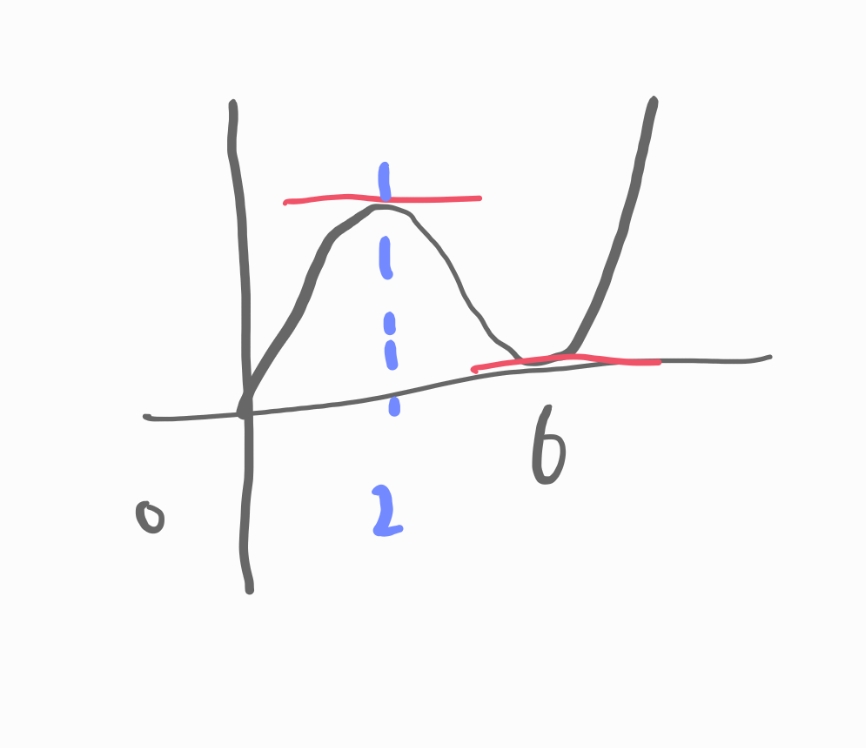
문제에서 두 점 사이의 거리는 [0, a] 구간에서 증가
[a, b] 구간에서 감소한다고 했고
t = a에서 t=b까지 점 Q의 움직인 거리를 구하라고 했으니,
Q점의 속도 그래프에서
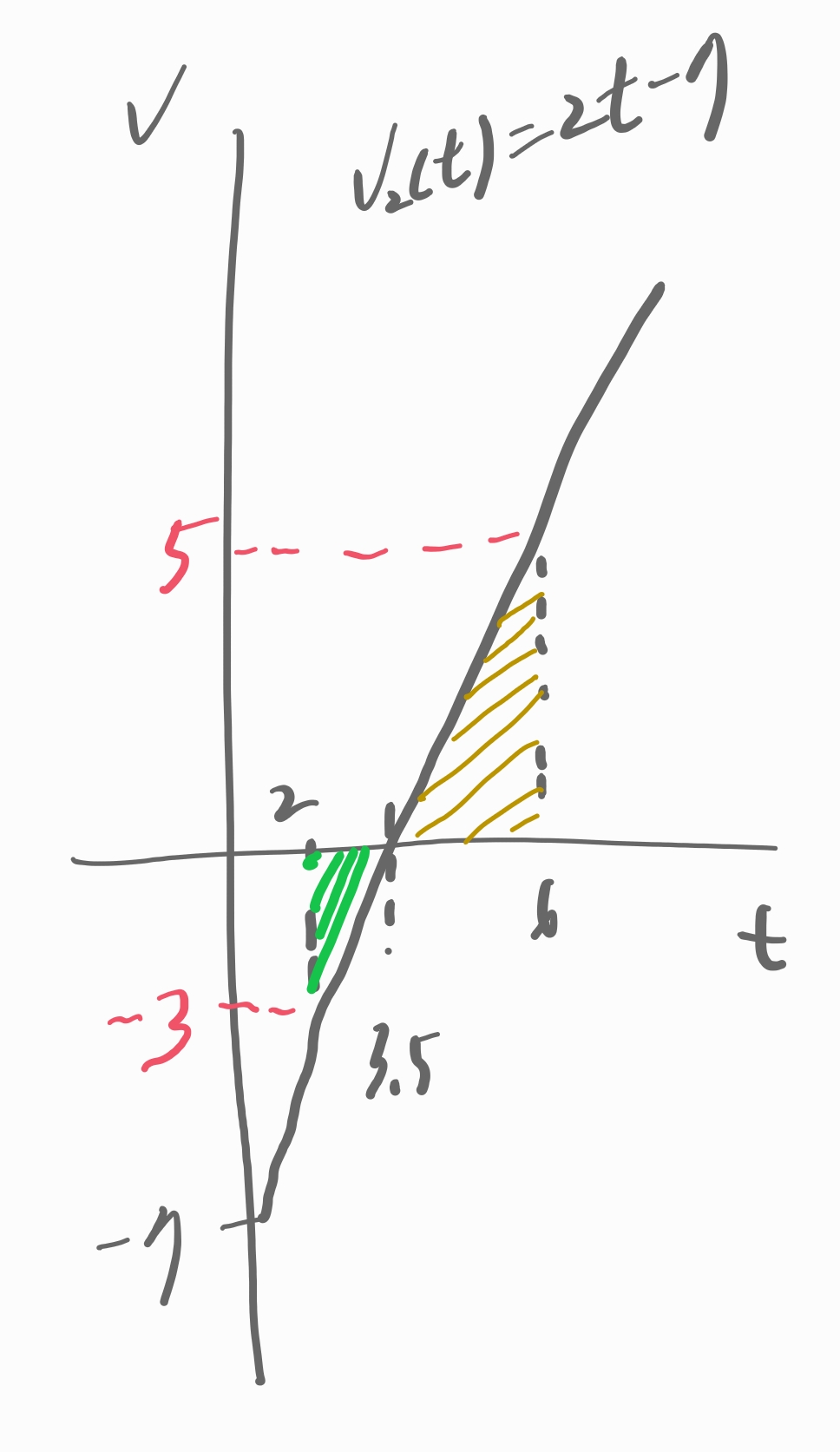
2초와 6초 동안 움직인 거리를 찾으면 됩니다.
거리 = 속도 × 시간 이기 때문에
위 그림에서 색칠된 면적을 구하면 됩니다.
두 직감삼각형의 면적을 각 각 구해서 더하면 답을 찾을 수 있습니다.
뭔가 엄청 멀리 돌아와서 답을 찾은 느낌입니다.
어쨌든 끝.
