24학년도 수학3번

 
24학년도 수학 세 번째 문제입니다.
3점짜리 문제입니다. 난도가 조금 올라간듯한 느낌적인 느낌입니다.
 

 
사인함수가 나왔습니다.
습관적으로 사인함수를 그려봅니다.

세타( θ )가 2분의3파이와 2파이 사이에서 사인함수는 음수(-)입니다...
.
.
.
잠간 고민하다가 사분면상에서의 사인값을 찾아볼 생각을 했습니다.
더 직관적으로 쉽게 접근할 수 있을 것 같습니다.
 

 
θ는 4사분면에 있습니다.
 
그럼 -θ는 반대로 돌려, 1사분면에서 사인값을 찾을 수 있습니다.
 

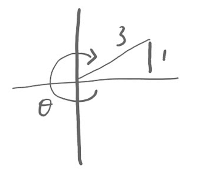
sin(- θ)가 3분의 1이라고 했으니,
1사분면에 그려지는 직각삼각형이 그려집니다.
 

다시 원래의 θ각에서 사인값을 찾아 직각삼각형을 그려봅니다.
빗변이 3
한 변이 -1입니다.(길이는 1이지만 음의 영역에 그려지니 음수로 표현합니다.)
나머지 한 변의 값을 구해보면,
루트 8 ; 8의 2제곱근이 되겠네요.
 

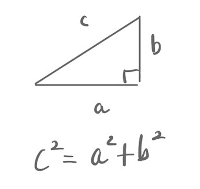
직각삼각형에서 빗변의 길이의 제곱은 다른 두변 각각을 제곱해서 더한 값과 같으니까요.
피타고라스 할아버지가 정리해 주신 값진 공식입니다.
 
.
.
.
아~! tan( θ)의 값을 구해야 하는군요.
 

 
막상 시도해 보니 생각보다 수월하게 풀렸습니다.
역시 그림을 적절히 그려주면 좋습니다.